Bonjour, je ne comprend un exo http://www.noelshack.com/2017-34-7-1503 ... apture.png
L'histoire de la L+1-ième ligne me perturbe un peu notamment , c'est la 1 ère fois que je vois ça
La somme sigma Bêta(i) L(i+1) (encadré sur la photo) elle représente quoi ? La somme de tout les éléments de la ligne ? La somme de tout les Bêta(i)*(les éléments de la ligne en question) ?
Besoin d'aide sur un exo d'algèbre linéaire
9 messages
- Page 1 sur 1
Re: Besoin d'aide sur un exo d'algèbre linéaire
attention, la numérotation des 'n' va de 0 à n soit n+1 termes.
c'est une matrice de taille (n+1)*(n+1), pas n*n
donc les lignes de la matrice sont notés de 1 à n+1 avec le décalage d'un indice
La ligne Li+1 est la ligne en dessous de la i ième ligne.
c'est une matrice de taille (n+1)*(n+1), pas n*n
donc les lignes de la matrice sont notés de 1 à n+1 avec le décalage d'un indice
La ligne Li+1 est la ligne en dessous de la i ième ligne.
Re: Besoin d'aide sur un exo d'algèbre linéaire
Oui j'avais remarqué ça , mon problème c'est que je ne comprend pas la notation L(i+1) , que représente t-elle dans cette somme? Comme passer de "L(i+1) aux Alpha(i) ?
Re: Besoin d'aide sur un exo d'algèbre linéaire
les Li sont des vecteurs
les sommes des betai Li+1 font 0
si tu exprimes P(alpha i), tu vas retomber sur chaque coordonnée (de la somme) des vecteurs betai Li+1 ... qui valent toutes 0.
les sommes des betai Li+1 font 0
si tu exprimes P(alpha i), tu vas retomber sur chaque coordonnée (de la somme) des vecteurs betai Li+1 ... qui valent toutes 0.
Modifié en dernier par pascal16 le 29 Aoû 2017, 06:32, modifié 1 fois.
Re: Besoin d'aide sur un exo d'algèbre linéaire
P(alpha i) = somme des Beta(i) alpha(i) (i variant de 0 à n)
donc en développant : P(alpha i)= Beta()alpha(0) +...+ Beta(n) alpha (n) ?
Je ne comprend pas ce que vous dites par "coordonnée des vecteurs betai Li+1 ... qui valent toutes 0."
Les coordonées du vecteur Li+1 avec i=0 sont 1,1,1...1
Li+1 avec i=2 : alpha0, alpha1 ...alpha n
donc en développant : P(alpha i)= Beta()alpha(0) +...+ Beta(n) alpha (n) ?
Je ne comprend pas ce que vous dites par "coordonnée des vecteurs betai Li+1 ... qui valent toutes 0."
Les coordonées du vecteur Li+1 avec i=0 sont 1,1,1...1
Li+1 avec i=2 : alpha0, alpha1 ...alpha n
Re: Besoin d'aide sur un exo d'algèbre linéaire
tu vas retomber sur chaque coordonnée de "la somme des vecteurs beta i Li+1"
Re: Besoin d'aide sur un exo d'algèbre linéaire
Bonjour,
En explicitant la somme :
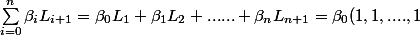 + \beta_1 (\alpha_0, \alpha_1, ..... \alpha_n)+.... +\beta_n (\alpha_0^n, \alpha_1^n, ..... \alpha_n^n))
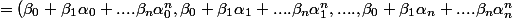=(0,0,.....,0)) .
.
Chaque coordonnée du vecteur est nulle, donc on retrouve bien que chaque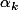 est racine du polynôme
est racine du polynôme  . Là encore attention de ne pas se mélanger car ils parlent de
. Là encore attention de ne pas se mélanger car ils parlent de =0) , et
, et  est déjà l'indice choisi dans la somme.
est déjà l'indice choisi dans la somme.
En explicitant la somme :
Chaque coordonnée du vecteur est nulle, donc on retrouve bien que chaque
Re: Besoin d'aide sur un exo d'algèbre linéaire
Juste autre chose, à la question 2 : P(j) = (X+ alpha(j))^n , il n'y a pas une petite faute? le "^n" ce ne serait pas "^j" ?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
