Besoin d'aide mathématiques financières

[pinkstar83]

Bonjour,

J'ai ce problème a traiter pour vendredi sur les emprunts, j'ai besoin de votre aide. je n'y arrive pas surtout aux questions 2 et 3. le 1 j'ai essayé mais je c sais pas trop !!!
Merci de votre aide

Problème :

Un particulier emprunte une somme de 50 000e au taux effectif global annuel hors assurance de 6%. Cet emprunt est remboursable par mensualités constantes, la première venant à échéance dans un mois.

1/ Calculer le montant de la mensualité si la durée de l'emprunt est de 15 ans.
2/ Décomposer et vérifier la 144eme mensualité.
3/ Calculer le montant de la mensualité si la durée de l'emprunt est infinie.

[Jonathan_]

je pense que sa doit etre un truc avec un terme geometrique, mais comme je suis pas genial en francais je sais pas ce que c'est un "taux effectif global annuel de 6%" ...tout les ans tu paye 6% de ce qui te restes a rendre?? c'est sa??

[pinkstar83]

Le TEG ( taux effectif gloabal) est le taux d'intéret sur l'emprunt par an. Des frais quoi !

[pinkstar83]

Donc qqn peut m'aider ou pas ?merci

[mathelot]

hello,
de manière générale, le "taux de l'argent à un an" permet de calculer la valeur future d'un capital par:
= valeur future
ou inversement, la valeur actuelle (d'aujourd'hui) d'un capital reçu seulement dans un an. par la formule:

La première chose à faire dans l'exo est de transformer ton TEG annuel
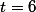en TEG mensuel par la formule:

ce qui donne un TEG mensuel
ce TEG mensuel est évidemment de l'ordre d'un douzième du TEG annuel.
Ensuite, concernant l'emprunt, pour le banquier, la valeur actuelle
de ses rentrées futures (les mensualités) sont égales à sa sortie de cash
d'aujourd'hui, le montant de l'emprunt. Ceçi donne l'égalité:

[mathelot]

Comme la formule précédente est la somme d'une progression géométrique:
la mensualité est donnée par:

soit, tous calculs faits:
m=417,65 euros

[mathelot]

ensuite, on peut programmer l'échéancier de l'emprunt (toutes les caculatrices financières l'ont comme routine de base)
K=capital emprunté=50000
=taux mensuel=0,486755
m=montant des mensualités=417,65
ne disposant pas de calculatrice financière, j'écris le petit programme:

0 ---> J
50000 ---> K
0,00486755 ---> T
417,65 --->M (mensualité)

WHILE J I (intéret)
K - (M-I) ---> K (capital remboursé)
J+1--->J
ENDWHILE
PRINT I
PRINT M-I
ce qui donne une décomposition de la 144ème mensualité en:
I=intérets=68.68 euros
M-I=capital remboursé=348.97 euros

[mathelot]

Pour la question (3), en cas d'emprunt infini, le montant m de la mensualité est
donnée par:

avec
d'après le principe de l'égalité de la valeur actuelle du cash reçu (emprunt) avec la somme des cash futurs (remboursements), actualisés à aujourd'hui, date de début. Ce principe est énoncé dans le post de 10h30.
Le se calcule aisémment.

[mathelot]

La mensualité m d'un emprunt infini est donc:


m=243,38 euros