Beppo Levi : utilisation simple
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 19 Déc 2017, 15:36
par chombier » 19 Déc 2017, 15:36
Bonjour,
je cherche une application directe du théorème de Beppo-Levi (en gros s'en servir pour calculer une intégrale).
J'ai trouvé un exercice qui semble correspondre : calculer

Il faudrait développer en série entière et utiliser Beppo Levi.
La réponse serait
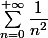
Est-ce que quelqu'un a une idée ?
Auriez-vous des exemples d'utilisation directe du théorème de Beppo-Levi ? Les séries entières positives ?
PS : J'ai trouvé cet exercice ici :
http://forum.mathematex.net/exercices-e ... 12292.html

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2017, 16:23
par Ben314 » 19 Déc 2017, 16:23
Salut,
C'est assez "couillon" :
^n= \sum_{m\geq1}\!xe^{-mx}\ \text{ (car } \ e^{-x}\!\in\,]0,1[\text{)})
.
Et tu n'a plus qu'à vérifier(à l'aide d'une intégration par parties) que
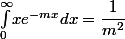
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 19 Déc 2017, 16:36
par chombier » 19 Déc 2017, 16:36
Merci Ben, il reste juste la partie qui m'intéressait au départ : justifier l'inversion signe intégrale / signe somme :
x}) dx = \sum_{n\geq1} \int_{0}^{\infty}(x e^{-(n-1)x}) dx)
C'est là que Beppo Levi nous sauve non ?
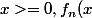=\sum_{k=1}^n {xe^{-(n-1)x}})
est une suite de fonctions croissante (série à terme positifs), intégrables, à valeur dans [

]

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2017, 17:36
par Ben314 » 19 Déc 2017, 17:36
Fait gaffe à ce que tu écrit :
Pour Beppo Lévy, ce qu'il faut (et c'est ce que tu as), c'est une suite croissante de fonctions (à ne pas confondre avec une suite de fonctions croissantes ce qui n'a franchement rien à voir).
Sinon, effectivement, le plus rapide ici pour justifier l'interversion limite/intégrale, c'est Pebbo-Levi (on peut aussi le faire via de la C.V. uniforme sur des compacts bien choisi, mais c'est passablement plus long).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 19 Déc 2017, 17:53
par chombier » 19 Déc 2017, 17:53
Merci Ben. Je cherchais une utilisation concrete de Beppo Levi, j'en ai trouvé une. C'est sans doute pas la plus simple mais j'en ai au moins une.
J'aimerais quand même bien arriver à bricoler un cas d'utilisation simple. Je résume :
Pour Noël, je voudrais :
- Une suite croissante (f_n) de fonctions mesurables à valeur dans R+ qui converge simplement vers une fonction f
- Que l'on sache calculer intégrer les f_n
- Que l'on ne sache pas intégrer f
Enfin bref, il faut qu'on gagne de l'information en utilisant Beppo Levi.
J'ai beau me triturer le cerveau dans tous les sens, impossible de faire émerger un cas simple d'utilisation.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2017, 18:26
par Ben314 » 19 Déc 2017, 18:26
Il te va pas celui là comme "cas simple" ?
Parce que
- Le premier truc qui vient à l'esprit pour avoir une somme croissante, c'est évidement une série à terme positifs
- La première série (convergente) qui vient à l'esprit, c'est la somme des q^n avec q>0.
- Sauf qu'il faut q<1 et que ça semble pas sot de prendre q=exp(-x) pour pas avoir à s'emmerder
(et de toute façon, si dans ton intégrale tu fait le changement de variable q=exp(-x), tu te ramène à une intégrale sur [0,1] avec exactement les même propriétés et beppo-levy marchera tout pareil)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 126 invités
