Bases duales
J'ai compris qu'on a
B' = (f1,...,fn) = (a*1,...,a*n)
et on cherche B*' = (a1,...,an) telle que
a*i(a1) = delta (i,j)
Or on a phi (v) = (f1(v),...,fn(v)) = (a*1(v),...,a*n(v))
et donc phi(ai) = (0,..,0,a*i(ai),0,...,0) = (0,..,0,1,0,..,0) = base canonique de Kn
Mais je ne vois ce qu'on peut en déduire sur la base B'*
B' = (f1,...,fn) = (a*1,...,a*n)
et on cherche B*' = (a1,...,an) telle que
a*i(a1) = delta (i,j)
Or on a phi (v) = (f1(v),...,fn(v)) = (a*1(v),...,a*n(v))
et donc phi(ai) = (0,..,0,a*i(ai),0,...,0) = (0,..,0,1,0,..,0) = base canonique de Kn
Mais je ne vois ce qu'on peut en déduire sur la base B'*
tu cherche une base de V, que tu appeles A.
d'apres ce qui precede, elle amet une base duale A* dans V*.
ce que tu veux c'est que A*=B'.
tu cherches donc ce que veut dire A*=B'.
pour ca tu prends la definition de ta base duale.
=\delta_{i,j}) pour tout i et j de 1 ... n
pour tout i et j de 1 ... n
si A*=B' tu dois avoir pour tout i de 1...n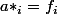 .
.
tu dois donc avoir=\delta_{i,j}) pour tout i et tout j de 1 ...n
pour tout i et tout j de 1 ...n
d'apres la definition de ca veut dire pour tout j de1...n
ca veut dire pour tout j de1...n =u_j)
ou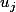 est le vecteur de
est le vecteur de 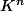 dont seule la j eme composante est non nulle et vaut 1.
dont seule la j eme composante est non nulle et vaut 1.
les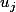 formant une base de
formant une base de 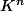 et
et  un isomorphisme, tu as bien l'existance de la base A, qui est l'image reciproque de la base U de
un isomorphisme, tu as bien l'existance de la base A, qui est l'image reciproque de la base U de 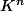 .
.
d'apres ce qui precede, elle amet une base duale A* dans V*.
ce que tu veux c'est que A*=B'.
tu cherches donc ce que veut dire A*=B'.
pour ca tu prends la definition de ta base duale.
si A*=B' tu dois avoir pour tout i de 1...n
tu dois donc avoir
d'apres la definition de
ou
les
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
