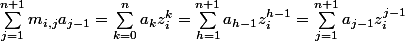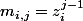Bases duales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 27 Oct 2010, 13:59
par arnaud32 » 27 Oct 2010, 13:59
avec la forme de M que je vous ai donne au dessus, reflechisser a ce que ca represente pour theta.
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 27 Oct 2010, 14:29
par sarah79 » 27 Oct 2010, 14:29
M=
1 z1 z1² .... z1^n
.
..
1 zn zn² ..... zn^n
et teta(P)=
(somme des ak(z1)^k,..., somme des ak(zn+1)^k)
j'ai cru que teta(p) était égale a la somme des coefficients des lignes de la matrice sauf que teta(P) va jusqu'a n+1 donc je vois pas
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 27 Oct 2010, 14:31
par sarah79 » 27 Oct 2010, 14:31
Dans la matrice M que vous nous avez donné vous dites que i et j vont de 1 à n+1
donc la dernière ligne de la matrice devrait etre
1 z(n+1) ....z(n+1)^n
non?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 27 Oct 2010, 14:44
par arnaud32 » 27 Oct 2010, 14:44
non
avec les notations precedentes
tu as
 =)
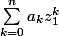
...
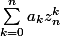
_i = \sum_{j=1}^{n+1}m_{i,j}a_j)
_i = \sum_{j=1}^{n+1}z_i^{j-1}a_j)
_i = \sum_{j=0}^{n}z_i^{j}a_j)
et
)_i = (M.a)_i)
donc M represente

dans les bases canoniques .
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 28 Oct 2010, 12:29
par sarah79 » 28 Oct 2010, 12:29
Je bloque toujours a la question d, on cherche la matrice qui représente teta(P) dans la base canonique de Cn[X] qui est (1,X,X²,...,X^n)
P(X)=somme des ak*X^k de k=0 à n
teta(P(X))=(a0+a1X+...+anX^n)
donc matrice de teta dans la base canonique Cn[X] : Mat(teta)= (a0,a1,..an) c'est ça si j'ai bien compris?
par contre la matrice dans Cn+1, je bloque un peu
on a teta(P)=
(a0+a1*z1+..+an*z1^n, ...,a0+a1*zn+1+,...,an*zn+1^n)
Pour trouver la matrice dans Cn+1 il faut que teta(p)=M*matrice de la base canonique de Cn+1 où M c'est la matrice que l'on cherche
Si je procède comme ça je vais trouver M ou c'est faux?
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 28 Oct 2010, 12:38
par sarah79 » 28 Oct 2010, 12:38
arnaud32 a écrit:ta matrice c'est
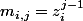
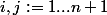
c'est a dire

...
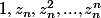
Ca c'est la deuxième matrice que l'on cherche mais je comprends pas comment on la trouve y a quelque chose qui m'échappe
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2010, 12:45
par arnaud32 » 28 Oct 2010, 12:45
theta est une application de
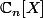
dans
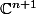
ca matrice est donc de quelle dimension?
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 28 Oct 2010, 12:47
par sarah79 » 28 Oct 2010, 12:47
la matrice est de dimension n+1*n+1
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2010, 13:07
par arnaud32 » 28 Oct 2010, 13:07
tu dois donc chercher une matrice (n+1)x(n+1) et non un vecteur comme tu me l'a donne.
ecris un polynome P de
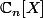
dans sa base canonique
ecris
)
dans la base canonique de
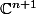
et pour passer de l'un a l'autre tu dois trouver ta matrice (n+1)x(n+1).
pour la trouver tu peux utilier ensuite
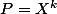
par ex.
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 28 Oct 2010, 13:12
par sarah79 » 28 Oct 2010, 13:12
je comprends rien on me demande décrire la matrice dans la base canonique de Cn[X] (au départ) et de Cn+1 (à l'arrivée) donc on cherche qu'une matrice mais je comprends pas d'habitude on dit écrire la matrice dans la base D mais là il parle de 2 bases ??
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 28 Oct 2010, 13:19
par sarah79 » 28 Oct 2010, 13:19
si P polynome de Cn[X] P est exprimé en fonction de X = a0+a1X+...+anX^n
teta(p) dans la base canonique de Cn+1 = a0+a1*z1+..+an*z1^n, ...,a0+a1*zn+1+,...,an*zn+1^n)
la c'est exprimé avec des z
comment je peut trouver une matrice qui permet de passer des X a des z?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2010, 14:03
par arnaud32 » 28 Oct 2010, 14:03
dans la base canonique de
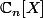
qui est
_{k=0...n})
le polynome
=\sum_{k=0}^{n}a_kX^k)
s'ecrit
)
ok?
dans la base canonique de
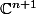
qui est (1,0,...,0) ... (0,...,0,1)
 = (P(z_1), ..., P(z_n)) =(\sum_{k=0}^{n}a_kz_1^k, ... , \sum_{k=0}^{n}a_kz_n^k))
maintenant tu dois trouver la matrice M
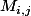
telle que
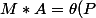)
M*A est un vecteur de
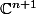
(attention les elements de
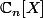
sont indices de 0 a n et ceux de
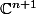
de1 a n+1)
donc pour tout i on a
_i = \sum_{j=1}^{n+1}m_{i,j}a_{j-1})
par definition du produit matriciel
et tu as
_i =(\theta(P))_i)
donc
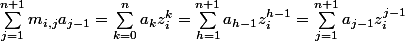
et donc:
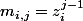
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 28 Oct 2010, 14:15
par sarah79 » 28 Oct 2010, 14:15
OK MERCI,je vais relire tout ça et essayer de bien tout comprendre
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
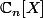 qui est
qui est _{k=0...n})
=\sum_{k=0}^{n}a_kX^k) s'ecrit
s'ecrit )
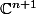 qui est (1,0,...,0) ... (0,...,0,1)
qui est (1,0,...,0) ... (0,...,0,1)  = (P(z_1), ..., P(z_n)) =(\sum_{k=0}^{n}a_kz_1^k, ... , \sum_{k=0}^{n}a_kz_n^k))
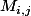 telle que
telle que 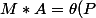)
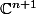
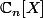 sont indices de 0 a n et ceux de
sont indices de 0 a n et ceux de 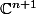 de1 a n+1)
de1 a n+1)_i = \sum_{j=1}^{n+1}m_{i,j}a_{j-1}) par definition du produit matriciel
par definition du produit matriciel_i =(\theta(P))_i) donc
donc