Est ce rigoureux de prendre Q dans K[X] et de montrer qu il existe une sous famille de {
Base de polynome
3 messages
- Page 1 sur 1
base de polynome
Bonsoir , j'ai un petit problème avec un exercice d algèbre voila : On me donne { n appartenant a N} avec deg(
n appartenant a N} avec deg(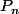=n) et on me demande de montrer que cette famille est génératrice de K[x]
et on me demande de montrer que cette famille est génératrice de K[x]
Est ce rigoureux de prendre Q dans K[X] et de montrer qu il existe une sous famille de {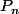 ,n appartenant a N} qui est génératrice de
,n appartenant a N} qui est génératrice de  [X] ?
[X] ?
Est ce rigoureux de prendre Q dans K[X] et de montrer qu il existe une sous famille de {
Re: base de polynome
Salut,
C'est pas très bien formulé.
Donc tu considères une famille (fixée) de polynômes à coefficients dans un corps K telle que pour tout n, on ait
de polynômes à coefficients dans un corps K telle que pour tout n, on ait =n) et tu souhaites montrer que la famille
et tu souhaites montrer que la famille est une famille génératrice de
est une famille génératrice de  espace des polynômes à coefficients dans
espace des polynômes à coefficients dans 
Je pense que ton idée est bonne.
Tu prends et tu notes
et tu notes  son degré.
son degré.
On considère la famille qui est une famille de polynômes de
qui est une famille de polynômes de  espace des polynômes de degré inférieur ou égal à r.
espace des polynômes de degré inférieur ou égal à r.
Cette famille est libre (montre le, c'est classique, ça provient du fait que les polynômes ont des degrés deux à deux distincts), c'est donc une base de (dû à son nombre d'éléments)
(dû à son nombre d'éléments)
Je te laisse conclure.
C'est pas très bien formulé.
Donc tu considères une famille (fixée)
Je pense que ton idée est bonne.
Tu prends
On considère la famille
Cette famille est libre (montre le, c'est classique, ça provient du fait que les polynômes ont des degrés deux à deux distincts), c'est donc une base de
Je te laisse conclure.
Pseudo modifié : anciennement Trident2.
Re: base de polynome
Salut,
Juste une petite remarque : on peut procéder comme le dit Trident et ça fait utiliser de jolis résultats d'algèbre linéaire, mais on peut aussi procéder de façon directe en montrant, par récurrence sur le degré de Q, que tout polynôme Q est combinaison linéaire des Pn : Si d°(Q)=k, comme d°(Pk)=k, il existe un scalaire lambda tel que Q-lambda.Pk est de degré <k (avec lambda=coeff_dominant_de_Q/coeff_dominant_de_Pk).
C'est évidement moins joli, mais ça donne un algo. "concon" pour trouver les coordonnées de Q dans la base (Pn).
Juste une petite remarque : on peut procéder comme le dit Trident et ça fait utiliser de jolis résultats d'algèbre linéaire, mais on peut aussi procéder de façon directe en montrant, par récurrence sur le degré de Q, que tout polynôme Q est combinaison linéaire des Pn : Si d°(Q)=k, comme d°(Pk)=k, il existe un scalaire lambda tel que Q-lambda.Pk est de degré <k (avec lambda=coeff_dominant_de_Q/coeff_dominant_de_Pk).
C'est évidement moins joli, mais ça donne un algo. "concon" pour trouver les coordonnées de Q dans la base (Pn).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
