Base de matrices

[george369]

Bonjour,

j'ai une question sur le problème suivant :

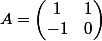
on a et aussi le centre de par rapport à A où K est un corps (donc l'ensemble des matrices carrées de coté 2 qui commutent avec A).

Le but est d'en calculer une base. Donc je résous l'équation par le pivot de gauss pour une matrice quelconque X dans :



je trouve des conditions sur les éléments de X (2 paramètres). On les note par exemple a, b, -a + b et -b.

Comment est-ce que j'en déduis une base, sachant que est de dimension 4 ?

[Ben314]

Salut,
Tu as quasiment la réponse a ta question. Il te suffit d'écrire que :

Pour avoir une base de l'ensemble des matrices X qui commute avec A (et cela montre bien sûr que ce s.e.v. est de dimension 2).

P.S. Sauf que mon petit doigt me dit que tu t'est trompé dans les calculs car, parmi les matrices qui commutent avec A, il y en a deux trés trés simples et elle ne font pas parti de tes solutions...

[george369]

Merci bien pour ta réponse.

d'une part sache que je n'ai pas mis les vrais résultats j'ai juste choisi les a et les b aléatoirement pour avoir le résultat en général (d'où le 'par exemple' dans mon message précédent. La vraie solution étant



J'ai vérifié ça marche. En fait il s'agit presque plus d'un problème de rédaction.

Le seul souci c'est qu'en cours on a appris que est de dimension qp. Il me faut donc une base à 4 éléments, non?

Est-ce que ce que tu me proposes correspond à cela ? J'ai du mal à comprendre s'il faut considérer les matrices comme des éléments ou comme des ensembles d'éléments, surtout dans l'ensemble des matrices ^^'.

J'avais pensé à mettre la base suivante :

[Doraki]

Mq,p(K) est de dimension q*p oui, mais toi tu cherches une base d'un sous-espace vectoriel de ça donc qui sera de dimension plus petit. Dans ton cas, c'est de dimension 2 vu que ta base a 2 éléments.

Tu as trouvé un isomorphisme de R² dans C(A) qui au couple (a,b) associe ta matrice en fonction de a et b.
Une base de R² c'est par exemple {(a=1,b=0),(a=0,b=1)}, et t'as plus qu'à regarder l'image de cette base par ton isomorphisme pour avoir une base de C(A).

Si t'avais 4 éléments dans ta base bah ça voudrait dire que C(A) = l'ensemble des matrices 2*2 tout entier.

[george369]

OK d'accord je vois le problème.

Est-ce que du coup dans le cas général on déduit la dimension de la base du nombre de paramètres trouvés dans l'équation ?

[EDIT:] question bête en fait vu qu'on a trouvé un isomorphisme de R² dans C(A). Ca répond à la question.

Merci bien pour votre aide !