Base image .

[naruto-next]

Salut,

j'ai une fonction lin de R3 sur R3 . Mon problème ce trouve au moment ou il faut trouver une base de imf

la matrice de f dans la base canonique vaut :

18 -18 -16
6 -6 -6
15 -15 -13

donc pour que appartiennent a imf alors
18 -18 -16| a
6 -6 -6 | b
15 -15 -13 | c

j'en arrive rapidement a une equation :

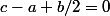
implique qu'il y a des solutions sinon non .
donc c'est la que j'ai du mal . je veux une base :

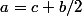
donc une base serait

serait une base ??

ou encore avec l'equation du debut je peux dire c = a - b/2
donc est aussi une base ??

[Manny06]

Salut,

j'ai une fonction lin de R3 sur R3 . Mon problème ce trouve au moment ou il faut trouver une base de imf

la matrice de f dans la base canonique vaut :

18 -18 -16
6 -6 -6
15 -15 -13

donc pour que appartiennent a imf alors
18 -18 -16| a
6 -6 -6 | b
15 -15 -13 | c

j'en arrive rapidement a une equation :

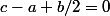
implique qu'il y a des solutions sinon non .
donc c'est la que j'ai du mal . je veux une base :

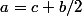
donc une base serait

serait une base ??

ou encore avec l'equation du debut je peux dire c = a - b/2
donc est aussi une base ??

je necomprends pas ce que tu fais
Imf est engendre par les 3 vecteurs f(i) f(j) f(k)
or f(j)=-f(i) donc ces deux vecteurs ne sont pas indépendants
tu peux donc voisir comme base f(i) soit (18;6;15) et f(k) soit (-16;-6;-13)

[naruto-next]

je veux une equation de l'image de f et une base .

donc pour tout vecteur (a , b , c ) appartient a im(f) cela implique

18x - 18y -16z = a
6x -6y -6z = b
15x -15y -13z = c

ca m'amene à c - a + b/2 = 0 la suite et au premier poste

[nidalinho]

je veux une equation de l'image de f et une base .

donc pour tout vecteur (a , b , c ) appartient a im(f) cela implique

18x - 18y -16z = a
6x -6y -6z = b
15x -15y -13z = c

ca m'amene à c - a + b/2 = 0 la suite et au premier poste

ouii c est juste car ona rgf=2 donc Imf est engendre par 2 vecteur (1,0,2)est (1,2,0)