[L1] Base d'un espace vectoriel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 09 Sep 2010, 19:15
par benekire2 » 09 Sep 2010, 19:15
Bonjour,
J'ai actuellement un problème sur un énoncé que voici :
On souhaite montrer que la famille
^n\)_{0 \le k \le n})
est une base de

1. Montrer qu'il suffit de montrer la liberté de la famille (fait)
2. On considère maintenant
_{0 \le k \le n}\in \mathbb{K}^{n+1})
. Supposons
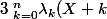^n=0)
a. Montrer que
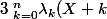^p=0)
pour tout

b. Montrer que

pour tout
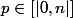
c. Montrer que pour tout P de R_n[X]
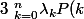=0)
d. Conclure.
J'ai donc un problème sur la 2.a. Comment dois-je faire ? J'espère que c'est pas une division par (X+k)^(n-p) ....
Pour la b il faut prendre X=0 pour la c ça se fait par combinaisons linéaires
Merci à vous !
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 09 Sep 2010, 19:19
par Finrod » 09 Sep 2010, 19:19
Si tu prend p=0 dans le 2 a tu obtiens juste que la somme des

est nulle, pas que chaque

est nul.
Pour le 2a, met juste en facteur le
^{n-p})
, il est non nul...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Sep 2010, 19:23
par Nightmare » 09 Sep 2010, 19:23
Salut,
on ne peut pas mettre (X+k)^(n-p) en facteur puisqu'il contient k qui varie donc dans la somme.
Je propose simplement de dériver.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 09 Sep 2010, 19:24
par benekire2 » 09 Sep 2010, 19:24
Salut Finrod, j'ai viré la deuxième question quand j'ai vu a quel point elle était stupide :zen:
EDIT: Merci nightmare ! En dérivant p fois on se retrouve avec un truc qui nous fournit le résultat,
Soit E le sous espace vectoriel des applications de R dans R , engendré par les fonctions x --> sin(kx) avec k dans [|1,n|] Déterminer une base de E.
J'aimerais bien montrer que les sin(kx) sont linéairement indépendants mais j'y parvient pas trop.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Sep 2010, 19:37
par Nightmare » 09 Sep 2010, 19:37
Hello,
la famille est bien libre, ça se fait bien par récurrence et ... en dérivant :lol3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 09 Sep 2010, 19:43
par benekire2 » 09 Sep 2010, 19:43
Tient, ça se fait souvent en dérivant sur les histoires de familles libres ... :zen:
Merci !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Sep 2010, 23:13
par Nightmare » 09 Sep 2010, 23:13
Ici, ça pourrait même se résoudre en intégrant, plus ou moins.
Hint : Calculer
sin(qx)dx)
pour p et q entiers.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 10 Sep 2010, 22:25
par benekire2 » 10 Sep 2010, 22:25
Nightmare >> En cherchant hier j'avais trouver cette méthode aussi , merci ^^
J'ai une autre question, Je considère f l'endomorphisme P --> P(X)+P(X+1) de K_n[X]
Je montre que Ker f =0 et que par conséquent f est un automorphisme de K_n[X]
Pour déterminer Ker(f-2Id) et Im(f-2Id) j'y vais à la barbare où il y a un truc plus fin ?
Merci à vous !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Sep 2010, 22:50
par Ben314 » 10 Sep 2010, 22:50
Salut,
Je ne sais pas ce que tu appelle "y aller à la barbare", mais si tu regarde ce que signifie (f-2Id)(P)=0 pour un polynôme P, tu devrait trouver une façon simple de trouver les polynômes P qui vérifient une telle équation (à condition que le corps de départ soit Q,R ou C, si c'est un corps de caractéristique p, c'est un peu plus tordu).
Une fois que tu as le noyeau, ça te donne la dimennsion de l'image, et avec un tout petit peu d'imagination, tu devrait voir immédiatement qui est l'image de f (une fois sa dimension connue).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 10 Sep 2010, 23:01
par benekire2 » 10 Sep 2010, 23:01
Salut ben !
Alors bah ça signifie qu'on cherche tout les polynômes P ( a coeff dans R ou C ) tels que P(X)+P(X+1)=2P
Sauf que moi j'ai écrit que
+P(X)= \Bigsum_{k=0}^{n}a_k(C_n^k+1)X^k)
Et donc je me retrouve avec une égalité de coefficients, qui implique que les a_k sont nuls ou alors que

ce qui se produit lorsque k=0,n
Cela dit le noyau de f-2Id n'est pas engendré par (1,X^n) ...
PS. Oula .. je crois que j'ai planté le calcul de P(X)+P(X+1) ... Je vais aller me coucher !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Sep 2010, 23:13
par Ben314 » 10 Sep 2010, 23:13
Bon, déjà, effectivement, on peut appeler ça "y aller à la barbare" et tu as du te gourrer quelque part car P(x)=X^n n'est pas dans le noyau de f.
Il me semble que d'écrire que P est dans Ker(f) si et seulement si P(X)=P(X+1) est suffisant : cela implique (dans Q, R ou C) que P est constant.
Pourquoi ?
Indication :
1) Que sait tu du nombre maxi de racine d'un polynôme de degrés n non nul ?
2) Combien de fois (au max) un polynôme non constant peut-il prendre une valeur donnée ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 10 Sep 2010, 23:17
par benekire2 » 10 Sep 2010, 23:17
Ouais si P(X)=P(X+1) alors P est constant ok, mais là c'est Ker(f-2ID) qu'on veut je cherche donc les P tels que P(X)+P(X+1)=2P(X)
Cela dit, le fait que j'écrive ça montre que P(X)=P(X+1) et j'en tire P K_0[X] :cry:
Effectivement, Dim Ker(f-2Id)=1 et donc Im(f-2Id) est un hyperplan, je vais réfléchir et finnir, merci bien !!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Sep 2010, 23:22
par Ben314 » 10 Sep 2010, 23:22
En reregardant ton post, effectivement,
+P(X))
n'est absolument pas égal à
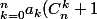X^k)
...
Edit : Sait tu montrer "proprement" que P(X+1)=P(X) implique que P est constant ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Sep 2010, 08:35
par benekire2 » 11 Sep 2010, 08:35
Oui en effet je m'étais rendu compte que c'était pas du tout bon pour P(X)+P(X+1) ...
Cela dit pour la preuve que tu me demande :
Les polynômes constants sont évidemment solutions. Soit P un polynôme non constant vérifiant P(X)=P(X+1). Clairement si xC est racine alors x+1 est également racine, i.e tous les x+k sont des racines de P.
Du coup P admet une infinité de racines qui sont toutes distinctes car pour tout (x,k)C X R* x+k est différent de x ; ainsi P est le polynôme nul i.e un polynôme constant, ce qui était exclu => Contradiction.
Cependant pour le problème, j'ai Ker(f-2Id)=K_0[X] et donc dim Im(f-2Id)=n i.e Im(f-2Id) est un hyper-plan, sauf que bah j'arrive pas trop à le déterminer,
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Sep 2010, 10:33
par Nightmare » 11 Sep 2010, 10:33
Attention, les polynômes constants sont aussi solutions !
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Sep 2010, 11:19
par benekire2 » 11 Sep 2010, 11:19
Salut nightmare !
C'est bien ce que j'ai dit dans la première phrase :we:
Par contre pour Im(f-2Id) je trouve pas, comment faut faire ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Sep 2010, 11:28
par Doraki » 11 Sep 2010, 11:28
Tu peux toujours regarder en détail pour n=1 ou n=2 si t'as pas d'idée.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2010, 11:32
par girdav » 11 Sep 2010, 11:32
benekire2 a écrit:
Par contre pour Im(f-2Id) je trouve pas, comment faut faire ?
Pourquoi ne pas te servir de la base que tu introduis dans le premier message?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Sep 2010, 11:41
par benekire2 » 11 Sep 2010, 11:41
Je ne vois pas à quelle base tu fais référence girdav , celle du tout premier message ? C'est pas le même exo !
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Sep 2010, 11:48
par benekire2 » 11 Sep 2010, 11:48
Mais chui complètement aveugle , c'est pourtant arhi évident,
=\mathbb{K}_{n-1}[X])
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
