Base dans un Hilbert
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
switch_df
- Membre Relatif
- Messages: 107
- Enregistré le: 21 Mar 2008, 17:20
-
 par switch_df » 07 Nov 2009, 09:48
par switch_df » 07 Nov 2009, 09:48
Salut tout le monde,
Voila un petit problème sur lequel je bloque pour conclure.
Soit H un Hilbert et
)
base de H. Un système orthonormale
)
est base de H ssi
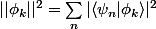
J ai montré l'implication directe avec l inégalité de Bessel et la projection orthogonal sur une espace contenu dans H. J ai aussi montré que
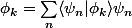
. Je pensais pouvoir conclure que les
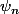
était une base hilbertienne avec cette relation, mais je n y arrive pas...
Si qqun a une idée, ce serait sympa.
A plus
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Nov 2009, 10:38
par Nightmare » 07 Nov 2009, 10:38
Salut !
A priori si
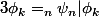\psi_{n})
c'est donc que
)=Vect((\psi_{i})))
non? C'est donc que la famille des psi est génératrices et vu qu'elle est orthonormale c'est une base de Hilbert.
-
switch_df
- Membre Relatif
- Messages: 107
- Enregistré le: 21 Mar 2008, 17:20
-
 par switch_df » 07 Nov 2009, 12:00
par switch_df » 07 Nov 2009, 12:00
Je suis assez d accord sur le raisonnement qui dit que c est une famille génératrice orthonormale. Le truc c est que selon ma définition une base
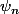
est hilbertienne ssi
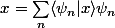
, et ça je vois pas comment le montrer.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Nov 2009, 12:18
par Nightmare » 07 Nov 2009, 12:18
Cette condition est équivalente au fait que la famille soit orthonormale et génératrice !
-
switch_df
- Membre Relatif
- Messages: 107
- Enregistré le: 21 Mar 2008, 17:20
-
 par switch_df » 07 Nov 2009, 13:33
par switch_df » 07 Nov 2009, 13:33
Je te crois volontiers, mais je ne vois pas vraiment pourquoi c est le cas. Y a t-il un moyen de le montrer?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
