Automorphismes intérieurs

par **Zebulon** » 02 Juin 2006, 09:51

Bonjour,
comment montre-t-on qu'un automorphisme f est un automorphisme intérieur? Est-ce s'il existe x appartenant au groupe tel que pour tout a appartenant à G,

?
Merci d'avance!

par **abcd22** » 02 Juin 2006, 12:01

Bonjour !
Un automorphisme intérieur est plutôt de la forme

pour tout a. :happy2:

par **Zebulon** » 02 Juin 2006, 15:01

Merci beaucoup!
C'était pour montrer que l'ensemble des automorphismes intérieurs était distingué dans Aut(G).
Soit

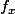
un automrphisme intérieur. Je veux montrer que quel que soit l'automorphisme g,

est un automorphisme intérieur.
Soit g appartenant à Aut(G) et soit a appartenant à G,

qui est bien un automorphisme intérieur.

par **abcd22** » 02 Juin 2006, 15:05

Oui c'est exact ! :happy3:

Automorphismes intérieurs

Automorphismes intérieurs

Qui est en ligne