Attracteurs étranges

par **Aspx** » 10 Jan 2008, 21:22

Bonsoir !

J'ai une question sur l'attracteur de Lorenz (c'est en partie l'objet de mon TIPE, j'ai posté ici car ça me semble le plus approprié) :

J'ai vu que l'on pouvait considérer la matrice du système (comme ds un système linéaire) et calculer valeurs propres, etc... J'aimerais savoir de quelle théorie il s'agit et aussi peut être quelques détails sur les systèmes d'équations différentielles dans le genre.

En espérant être pas trop vague, merci !

par **legeniedesalpages** » 10 Jan 2008, 21:34

salut, je suis pas sûr mais je pense qu'il s'agit de systèmes dynamiques ou théorie du chaos.

par **Aspx** » 10 Jan 2008, 21:57

Oui c'est bien ça, la théorie du chaos. Mais mon problême se limite à l'étude succinte de ce système différentiel.
Si vous avez plus d'informations sur la matrice du système peut être, je pense que c'est un bon parti pour commencer.

par **Dominique Lefebvre** » 10 Jan 2008, 22:27

Bonsoir,

Le système de Lorenz.. c'est un système du troisième ordre non-linéaire X'= F(X)
Il n'est pas intégrable analytiquement et on peut en dire que:

il est invariant sous la transformation (x,y,z) -> (-x,-y,z)
L'axe Oz,x=y=0 est un ensemble invariant
le système est dissipatif car div(F(X)) = -(sigma + 1 + beta) < 0
toutes les solutions sont bornées pour t tendant vers l'infini
ses points fixes sont les solutions des équations y=x , x(rho-z)-y = 0 et beta*z= -x² = 0

Si tu veux étudier sa stabilité, tu peux le faire par la méthode de linéarisation, en calculant les valeurs propres de la matrice jacobienne DF(X) en chacun des points fixes.

Nota : les paramètres valent dans le système de Lorenz
sigma = 10, beta = 8/3 et rho = 28 (ce sont des données issues d'EDO de météo)

par **Aspx** » 10 Jan 2008, 23:01

Génial merci beaucoup !
(Si vous avez d'autres suggestions d'approches du sujet n'hésitez surtout pas !)

par **Dominique Lefebvre** » 10 Jan 2008, 23:06

Aspx a écrit:Génial merci beaucoup !
(Si vous avez d'autres suggestions d'approches du sujet n'hésitez surtout pas !)

Tu peux aussi démontrer que le point fixe 0 = (0,0,0) est asymptotiquement stable si rho < 1 (méthode de la fonction de Lyapunov) et que c'est un attracteur sous cette condition et aussi que son bassin d'attraction est R^3

par **Aspx** » 10 Jan 2008, 23:11

Quelle est la propriété d'un système dissipatif ?
Qu'est-ce que le bassin d'attraction ? R^3 =

?

par **Dominique Lefebvre** » 11 Jan 2008, 09:37

Aspx a écrit:Quelle est la propriété d'un système dissipatif ?
Qu'est-ce que le bassin d'attraction ? R^3 = ?

systèm dissipatif : imagine un volume V(t) dans l'espace des phases du système.
On dit qu'un système est conservatif s'il conserve les volumes dans l'espace des phases ( V(t) = V(t0) pour tout v0 et tout t>t0

On dit qu'un système est dissipatif s'il ne conserve pas les volumes. Si V(t0) différent de 0, dans un système dissipatif, la limite de V(t) pour t tendant vers l'infini est 0. Les systèmes chaotiques sont des systèmes dissipatifs.

Pour définir un bassin, il faut d'abord définir un attracteur. Sa définition classique est "un compact de l'espace des phases, invariant par l'application, vers lequel toutes les trajectoires convergent".
On dit qu'un attracteur est étrange lorsque sa dimension est fractale (non entière).
Un bassin est l'ensemble des points dont les trajectoires convergent vers l'attracteur.

par **Aspx** » 11 Jan 2008, 18:36

Tout cela est vraiment très interessant et je pense pouvoir comprendre des notions, est-ce qu'il y aurait un cours disponible sur le sujet à disposition (j'ai éffectué des recherches mais c'est très difficile d'obtenir quelque chose de pertinent sur le sujet c'est pourquoi je m'en remet à vous).
Merci!

par **Dominique Lefebvre** » 11 Jan 2008, 18:58

Aspx a écrit:Tout cela est vraiment très interessant et je pense pouvoir comprendre des notions, est-ce qu'il y aurait un cours disponible sur le sujet à disposition (j'ai éffectué des recherches mais c'est très difficile d'obtenir quelque chose de pertinent sur le sujet c'est pourquoi je m'en remet à vous).
Merci!

Bonsoir,
Quelques documents:
[url="http://e2phy.in2p3.fr/2005/documents/apres_ecole/Textes/Manneville_txt.pdf"]http://e2phy.in2p3.fr/2005/documents/apres_ecole/Textes/Manneville_txt.pdf[/url]
[url="http://www.ladhyx.polytechnique.fr/people/pops/webptl.pdf"]http://www.ladhyx.polytechnique.fr/people/pops/webptl.pdf[/url]
[url="ftp://ftp.umh.ac.be/pub/ftp_polymers/pascal/Chaos_intro.pdf"]ftp://ftp.umh.ac.be/pub/ftp_polymers/pascal/Chaos_intro.pdf[/url]
[url="http://www.mathappl.polymtl.ca/steven/cours/MTH2210/Themes/Theme7.pdf"]http://www.mathappl.polymtl.ca/steven/cours/MTH2210/Themes/Theme7.pdf[/url]

par **Aspx** » 11 Jan 2008, 20:03

Qu'ai-je fait pour mériter un si bon traitement ? :doh:

Merci milles fois je suis aux anges !! :+++:

par **Dominique Lefebvre** » 11 Jan 2008, 20:29

Aspx a écrit:Qu'ai-je fait pour mériter un si bon traitement ? :doh:

Merci milles fois je suis aux anges !! :+++:

Rien, j'ai travaillé sur les systèmes chaotiques quantiques...

par **Aspx** » 11 Jan 2008, 20:59

Ca ne m'étonne pas c'est la première fois qu'on me répond aussi précisémment sur le sujet c'est vraiment génial ça m'ouvre pleins de perspectives pour mon sujet !

Comme ma présentation dure seulement dix minutes (avec un rapport de 5 pages max plus illustrations pour les ENS). Donc j'ai pas de quoi faire un truc qui regroupe beaucoup de notions liées au chaos.

Le but de mon sujet sera vraiment l'étude des mesures de la stabilité ou non de systèmes dynamiques avec une partie théorique (déf. et propriétés, théorie des ED d'ordre 3, stabilité, attracteur, exposant de lyapunov...) puis une partie illustration avec l'attracteur de Lorenz (application directe de l'étude théorique, approche expérimentale, algorithmes de tracé). Puis une conclusion avec une ouverture sur la théorie plus large des perturbations, le chaos, les fractals...

Merci beaucoup en tout cas j'ai tout pleins d'idées :id:
Ca me plait vraiment ce sujet, j'ai vraiment l'impréssion que c'est un concentré de beauté mathématique c'est... Bref.

(des fois j'ai du mal à m'imaginer ingénieur)

--------------------------------------------------------------------------

Pour en revenir aux questions (puisque tu connais le sujet je vais pas me priver, sans vouloir passer pour une sangsue) :

J'ai trouvé sur le net (de manière quasi-miraculeuse) l'énoncé (en anglais) d'un théorème dont j'ignore s'il possède un nom :
Soit

, et

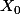
un point fixe du système

.
Le point est asymptotiquement stable (au sens de Lyapunov) ssi toutes les valeurs propres de A ont une partie réelle 0.

Quel est-il et comment le démontre on ?
Merci!

par **Dominique Lefebvre** » 11 Jan 2008, 22:39

Aspx a écrit:Pour en revenir aux questions (puisque tu connais le sujet je vais pas me priver, sans vouloir passer pour une sangsue) :

J'ai trouvé sur le net (de manière quasi-miraculeuse) l'énoncé (en anglais) d'un théorème dont j'ignore s'il possède un nom :
Soit , et un point fixe du système .
Le point est asymptotiquement stable (au sens de Lyapunov) ssi toutes les valeurs propres de A ont une partie réelle 0.

Quel est-il et comment le démontre on ?
Merci!

Regarde donc à la page 51, le théorème V.1:
[url="http://math.univ-lyon1.fr/~benzoni/EDO-M1.pdf"]http://math.univ-lyon1.fr/~benzoni/EDO-M1.pdf[/url]

Un conseil: procure toi le cours de Pierrette Benoist-Gueutal (Mathématiques pour la physique - Introduction à la théorie qualitative des systèmes dynamiques). Ce bouquin te sera très utile (Th 2.2 p 246 pour le théorème ci-dessus).

par **Aspx** » 11 Jan 2008, 22:58

Merci beaucoup ! Je vais avoir de la lecture je crois :lol2:
D'ici ma prochaine question je te remercie milles fois.

Attracteurs étranges

Attracteurs étranges

Qui est en ligne