Asymptote oblique

[mehdibj]

Bonsoir ,
pour le traçage d'une courbe j'ai besoin de déterminer les asymptote de celle ci alors vue que la fonction tend vers +infinie au voisinage de + infinie je fais :
je tombe sur 'e' alors quand je calcule ensuite :
je tombe sur +infinie !
qu'est ce que sa veut dire ? est ce j'ai fait une faute ou bien cela peut arriver ?
la fonction en question :
Merci d’avance

[pascal16]

si ce que tu as calculé est juste, ça veut dire que la fonction admet une direction asymptotique, mais pas une asymptote.


Mais :
f(x) = x*exp( 1-1/(x-2))
= e.x.(exp(-1/(x-2))
= e.x.(1-1/(x-2) + o(1/x))
=e.x - e + o(1)

[mehdibj]

si ce que tu as calculé est juste, ça veut dire que la fonction admet une direction asymptotique, mais pas une asymptote.


Mais :
f(x) = x*exp( 1-1/(x-2))
= e.x.(exp(-1/(x-2))
= e.x.(1-1/(x-2) + o(1/x))
=e.x - e + o(1)

d'accord donc je ne peux pas utiliser cette information pour tracer la courbe , merci beaucoup.

[pascal16]

si, tu as une erreur de calcul :

lim f(x)-ex = -e

f(x) - ex = x*exp( 1-1/(x-2)) - ex
= x.e.exp( -1/(x-2)) -ex
= ex(exp1 ( -1/(x-2)) -1)

de la forme exp(t) - 1 avec t ->0, exp(t) - 1 tend vers t
lim = lim ex(-1/(x-2)) = -e

[rcompany]

si ce que tu as calculé est juste, ça veut dire que la fonction admet une direction asymptotique, mais pas une asymptote.


Mais :
f(x) = x*exp( 1-1/(x-2))
= e.x.(exp(-1/(x-2))
= e.x.(1-1/(x-2) + o(1/x))
=e.x - e + o(1)

d'accord donc je ne peux pas utiliser cette information pour tracer la courbe , merci beaucoup.

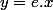
Pourquoi ne peut-on pas dire que la droite d'équation est asymptote de ?

[chan79]

on peut poser y=(x-1)/(x-2)
tu dois arriver à y=ex+e pour l'asymptote

[pascal16]

Ma phrase commence par "SI", et ensuite je te dis qu'il y a une erreur dans tes calculs.

la droite y=ex-e est droite asymptote en +oo

[chan79]

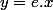
Pourquoi ne peut-on pas dire que la droite d'équation est asymptote de ?

je dirais ça:

[pascal16]

merci pour l'erreur, correction du signe
(x-1)/(x-2)=(x-2 + 1) / (x-2) = 1+ 1/(x-2)

f(x) - ex = x*exp( 1+1/(x-2)) - ex
= x.e.exp( +1/(x-2)) -ex
= ex(exp1 ( +1/(x-2)) -1)

de la forme exp(t) - 1 avec t ->0, exp(t) - 1 tend vers t
lim = lim ex(1/(x-2)) = +e

[chan79]

Pour la limite de quand x tend vers ou vers

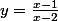
on peut poser ce qui donne
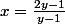
Quand x tend vers ou vers , y tend vers 1.
On cherche la limite quand tend vers 1 de:

Le quotient tend vers (limite du taux d'accroissement)
tend vers 1
La limite cherchée est