Associativité des barycentres

[T-T]

bonjour , je reste bloqué sur un exercice

On note X = bar {(x1,p1),....,(xn,pn)} et x={(x1,x2),.....(xn,pn)}

et je dois montrer l'associativité des barycentres : X=bar {(x,n) ,(x(k+1),p(k+1)),.....(xn,pn)}


je ne sais meme pas par quoi commencer

merci :)

[Nightmare]

Salut !

Ben déjà, il faudrait voir ce qu'on veut montrer. Qu'est-ce que pour toi l'associativité des barycentres?

[T-T]

hey bien par exemple

On a A=bar {(A,a),(B,b),(C,c) et D=bar{(A,a),(B,b)}

donc comme le barycentres est associative

on a A=bar{(D,a+b),(C,c)}

Pour moi c'est ca l'associativité des barycentres

[Nightmare]

Et dans le cas où l'on a n points?

[T-T]

A=bar {(a1,p1),.....(an,pn)} et B=bar{(a1,p1),....(ak,pk)}

avec k appartenant [1,n]

d'ou A={(a,p),(a(k+1),(a(k+1),p(k+1)),......,(an,pn)}

enfin la je recopie ce que j'ai mis au debut ...

[T-T]

on peut raisonner par récurrence?

[mathelot]

bonsoir,

ça marche exactement comme les moyennes, mais non pas avec des somme
de nombres mais des sommes de vecteurs.

k nombres comptent pour (où m est leur moyenne)
dans le calcul de la moyenne M de n nombres. ()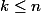


içi c'est pareil, on remplace par exemple
par
où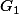 est le barycentre (nécessairement partiel) de A et B
dans un expression comme