Arithmétique

[dalhfire]

Bonjour,

Je suis en prépa PCSI et voici mon problème :



Je ne vois par où commencer ?

Merci d'avance
Cordialement
Dalhfire

[beagle]

décomposition en produit de nombres premiers de a,
soit ka un nombre premier de la décomposition de a,, alors ka n'est pas dans b,
et ce ka qui divise c ou bien c ou bien c ou bien c , ce ka il doit diviser un des k c,
bref il divise c et donc tous les c, et donc le facteur ka est en puissance k dans a
et c'est idem pour tous les premiers qui composent a

bref appeler cela ka n'était pas la variable la plus maligne, trouve une autre lettre.
remarque toi tu nous écrits a,b,c,d dans IN4 mais on n'a pas de d, on a k a la place?

[dalhfire]

Merci de votre reponse aussi rapide

Oui c'est bien un k et pas un d faute de frappe ^^

Quand vous dite :"ka un nombre premier de la décomposition de a" c'est k fois a ou k indice a ?
De plus on considère alors a non premier ?

[beagle]

a n'est pas premier, aet b sont premiers entre eux.

par contre il ya une gourrance quelque part dans mon truc
c'est que le ka premier dans a il peut ètre en puissance multiple de k

si tu prends un premier de a il peut ètre dans a à la puisance 2k ou 3k ou ik ...
j'ai pas le temps de voir quelle ligne faut rectifier.

en plus je sais pas rédiger ça proprement.
Bon je pense que l'idée sous-jaccente tu l'as ...
a toi d'ètre rigoureux!

[dalhfire]

D'accord je vais essayer de rédiger ca correctement.
Mais si je comprends bien "le facteur ka est en puissance k dans a" correspond à un terme qui compose le alpha finalement, et c'est la multiplication des différents facteurs ka qui donne alpha ?

[beagle]

on montre que i premier dans la décomposition de a, ben il est un des premiers dans la décomposition de c.
ensuite i est à une puissance donnée j dans c
et on a que que k x j est la puissance de i dans a, vu que b n'apporte pas de puissance de i

et ceci pour tous les ia de a

Je suis un peu fatigué je menmèle,
pis aussi je sais pas le rediger,
tu vois quand même?

[Ben314]

Salut,
A rédiger, c'est on ne peut plus "concon" :
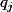
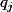
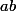
Si la décomposition en facteurs premiers de sont avec premiers distincts ; premiers distincts et , alors le fait que et sont premiers entre eux signifie que les sont distincts des donc ça dit très exactement que la décomposition en facteurs premiers de c'est .
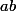
Or, comme , la décomposition en facteurs premiers de on peut aussi l'obtenir en prenant celle de : avec premiers distincts ; qui donne .
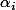
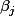
Et arrivé à ce point, l'unicité de cette fameuse décomposition permet d'en déduire que les et les , ce sont tous des , c'est à dire tous des multiples de ce qui signifie que et sont des puissances k-ième de nombre entiers.

Bref, en résumé, la soit disant "preuve", en fait, elle ne fait que "brasser du vent" et à peu prés tout le monde écrit simplement que "c'est évident via l'unicité de la décomposition en facteur premiers" plutôt que de se faire chier avec le type de jargon ci dessus et tout le charabia d'indices et d'exposant qui, au fond, ne rend pas franchement le truc plus clair, bien au contraire, ça donne l'impression que le truc est compliqué alors que c'est complètement évident mais que la symbolique mathématique "classique" (avec les indices et tout le bordel) n'est pas super adaptée pour transcrire le raisonnement.

[beagle]

sommes d'accord sur le évident, mais souvent les choses évidentes sont difficiles à écrire.

Là l'écriture permet quand même par rapport à mon blabla de prendre d'emblée toute la décomposition,
alors que j'ai commencé en prenant un seul facteur premier et qu'il fallait à la fin tous les réunir pour a et pour b,
enfin entre autres.
En prepa faut écrire de façon concise , donc l'écriture comme tu l'as mis Ben314
faut s'en inspirer je pense.
merci d'avoir repris!