Arithmétique

[houssamhoussni]

salut,
soit a et p 2 nombres premiers entre eux et p un nombre premier
montrez qu il existe r et v 2 entiers naturels tel p divise a^r-p^v!
(a^r est a à la puissance r)
merci d'avance!

[Ben314]

Salut,
Déjà, y'a pas le choix, il faut obligatoirement que v=0, sinon p diviserait p^v et devrait donc diviser a^r ce qui n'est pas possible vu que a n'est pas divisible par p.
Ensuite, si tu regarde les reste de division par p des différents a^r, tu va forcément tomber plusieurs fois sur le même reste (vu qu'il n'y a qu'un nombre fini de restes possibles) ce qui signifie qu'il existe r1>r2 tel que a^r1 et a^r2 ont le même reste de division par p donc que a^r1-a^r2 est divisible par p.
Or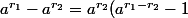 et, comme p ne divise pas c'est qu'il divise .