chombier a écrit:Presque... combien de valeurs différentes peuvent prendre i et j ?
(a+1)(b+1)
Arithmetique phi
35 messages
- Page 2 sur 2 - 1, 2
par adamNIDO » 07 Juin 2015, 17:49
(a+1)(b+1)
par zygomatique » 07 Juin 2015, 17:54
oui ...
maintenant généralise au produit de r nombres premiers ...
maintenant généralise au produit de r nombres premiers ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par adamNIDO » 07 Juin 2015, 19:07
paquito a écrit:n=18=2x3², soit 6 diviseurs dont 4 propres.Calcule
svp dis moi est ce que caculer le nombre de diviseur de n revient a calculer le phi
qui est ce que ca veut dire propres : les diviseurs premiers
si le cas on a que 2 a savoir: 2 3
par paquito » 07 Juin 2015, 19:20
adamNIDO a écrit:svp dis moi est ce que caculer le nombre de diviseur de n revient a calculer le phi
qui est ce que ca veut dire propres : les diviseurs premiers
si le cas on a que 2 a savoir: 2 3
Les diviseurs propres de n sont ceux qui sont différent de 1 et de n; tout diviseur propre de n ne peut être premier avec n!
donc il reste 5, 7,11, 13 et 17.
par adamNIDO » 07 Juin 2015, 19:36
paquito a écrit:Les diviseurs propres de n sont ceux qui sont différent de 1 et de n; tout diviseur propre de n ne peut être premier avec n!
donc il reste 5, 7,11, 13 et 17.
non cest 2 3 6 9
par adamNIDO » 08 Juin 2015, 15:26
paquito a écrit:TU TE FOUS DU MONDE!!!!!
non tu ma donner la defintion des diviseurs propres de n sont ceux qui sont différent de 1 et de n; tout diviseur propre de n ne peut être premier avec n!
et comme on a :
1 2 3 6 9 18 et dapres la definition que tu ma donner en dessus on a 4 propres 2 3 6 9 je suis desole si ma reponse n'est pas correct mais j'ai ecrit ce que je comprend
par adamNIDO » 08 Juin 2015, 18:17
d'apres l'image ne dessus on a
=\phi(2\times 9)=\phi(2)\times\phi(9)=(2-2^0)\times(3^2-3^1)=6)
mais je sais pas repondre a la question 2
mais je sais pas repondre a la question 2
par adamNIDO » 08 Juin 2015, 19:07
comme 
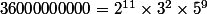
alors
le nombre de ces divisieurs cest
=\phi(2^{11}\times3^{2}\times5^{9})=\phi(2^{11})\times\phi(3^{2})\times\phi(5^{9})=(2^{11}-2^{10})\times(3^{2}-3^{1})\times(5^{9}-5^{8})=9600000000)
mais je sais pas comment faire une synthese pour repondre a la question 2
le nombre de ces divisieurs cest
mais je sais pas comment faire une synthese pour repondre a la question 2
par paquito » 09 Juin 2015, 04:39
adamNIDO a écrit:exist il pas un corrige detaille sur un pdf ?
C'est tellement plus facile de recopier un corrigé! Malheureusement, ça n'apporte pas grand chose!
par zygomatique » 09 Juin 2015, 08:13
il est triste de ne pas arriver à généraliser .... 
si
avec p et q premiers entre eux alors tout diviseurs de n est 
avec 
donc n possède (a + 1)(b + 1) diviseurs
si
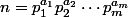
alors tout diviseurs de n est 
il y a donc autant de diviseurs de n que de m-uplets)
....
si
donc n possède (a + 1)(b + 1) diviseurs
si
il y a donc autant de diviseurs de n que de m-uplets
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
35 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :