Arithmétique - Nombres premiers
27 messages
- Page 2 sur 2 - 1, 2
Ca marche parfaitement bien et ça correspond à l'indic que j'avais mis plus haut :
1) On peut se passer de l'absurde en notant que tout diviseur premier de (N!)²+1 produit un nombre premier plus grand que N et congru à 1 modulo 4.
2) (j'insiste) On peut montrer que tout diviseurs premier de n²+1 est congru à 1 modulo 4 avec seulement le petit théorème de fermat :
Si p divise n²+1 alors p est impair et n²=-1 [p].
Or n^(p-1)=1 modulo p donc (-1)^((p-1)/2)=n^(p-1)=1 [p] d'où (p-1)/2 est pair.
Pour "l'Indice nodgim" de lapras (ou le contraire...), toujours avec le petit théorème de fermat, on montre que tout diviseur premier de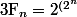}+1) est congru à 1 modulo
est congru à 1 modulo 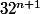
C'est légèrement plus compliqué comme exemple, mais ça démontre aussi légèrement mieux :
Pour tout entier k fixé, il y a une infinité de nombres premier congrus à 1 modulo .
.
Edit : J'avais pas "tourné la page" donc pas lu le post de Yos...
Juste pour te contrarier, je signale que :Ben314 a écrit:Pour les nombres premiers congrus à 1 modulo p, on peut aussi montrer que, pour tout n, les diviseurs premiers impairs de n²+1 sont tous congrus à 1 modulo 4 (à l'aide du petit théorème de Fermat)...
1) On peut se passer de l'absurde en notant que tout diviseur premier de (N!)²+1 produit un nombre premier plus grand que N et congru à 1 modulo 4.
2) (j'insiste) On peut montrer que tout diviseurs premier de n²+1 est congru à 1 modulo 4 avec seulement le petit théorème de fermat :
Si p divise n²+1 alors p est impair et n²=-1 [p].
Or n^(p-1)=1 modulo p donc (-1)^((p-1)/2)=n^(p-1)=1 [p] d'où (p-1)/2 est pair.
Pour "l'Indice nodgim" de lapras (ou le contraire...), toujours avec le petit théorème de fermat, on montre que tout diviseur premier de
C'est légèrement plus compliqué comme exemple, mais ça démontre aussi légèrement mieux :
Pour tout entier k fixé, il y a une infinité de nombres premier congrus à 1 modulo
Edit : J'avais pas "tourné la page" donc pas lu le post de Yos...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit: on montre que tout diviseur premier deest congru à 1 modulo
Oui, c'est la même difficulté (voire la même preuve) que pour les diviseurs de n²+1, donc le passage par les Fermats est pas très intéressant pour l'infinitude des premiers de la forme 4k+1.
Ben314 a écrit:ça démontre aussi légèrement mieux :
Pour tout entier k fixé, il y a une infinité de nombres premier congrus à 1 modulo.
Oui ça c'est pas mal.
Dans le même genre on a aussi "facilement" l'infinitude des premiers de la forme kp+1.
Comme "à froid" ça ne me disait rien, j'ai cherché...yos a écrit:Dans le même genre on a aussi "facilement" l'infinitude des premiers de la forme kp+1.
Je me demande si la généralisation de la méthode employée çi dessus n'est pas :
Sidésigne le a-ième polynôme cyclotomique (
) et
un entier premier avec
alors tout diviseur premier
de
est congru à 1 modulo
De plus, comme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
O.K., mais le "sans les cyclos" est un peu gonflé : il me semble quand même que, pour p premier,yos a écrit:Sans les cyclos :
1) Soit p un nombre premier et. Montrer que les diviseurs premiers de
sont congrus à 1 modulo p.
2) Conclure.
Sauf erreur, tu peut même prendre 1+a+a²+...a^(p-1) où a est un entier quelconque tel que p ne divise pas a-1 (ce qui fait que je me demande si je me suis pas gourré de condition dans mon théorème du post çi dessus : je vais refaire les calculs vu que j'ai déjà foutu les feuilles à la poubelle...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
27 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
