Arithmétique - Nombres premiers
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Avr 2010, 10:29
par benekire2 » 20 Avr 2010, 10:29
Bonjour,
J'ai un soucis dans un exercice que je n'arrive pas à résoudre. L'énoncé ne doit pas être très compliqué, mais je vois pas trop comment débuter. Une démonstration par l'absurde ?
Voici l'énoncé :
Démontrer qu'il existe une infinité de nombre premiers congrus à -1 modulo 4.
Merci beaucoup :id:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Avr 2010, 10:46
par Ben314 » 20 Avr 2010, 10:46
Effectivement, l'absurde parrait le plus simple (mais on peut s'en passer) et, s'il y en avait un nombre fini, on est évidement tenté d'en faire ...
Ensuite, il est bon de noter qu'in nombre congru à -1 modulo 4 contient forécement un nombre premier congru à -1 modulo 4 dans sa décomposition en facteurs premiers.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Avr 2010, 12:48
par benekire2 » 20 Avr 2010, 12:48
Ba je vais dire qu'il n'y en a qu'un nombre fini et essayer de trouver une contradiction. Un peu comme dans la démo de l'infinité des nombres premiers ( une des démos ...) merci beaucoup
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 20 Avr 2010, 14:51
par lapras » 20 Avr 2010, 14:51
Salut,
c'est exactement la même idée que la démo d'infinité classique, juste on change un peu la formule. (celle que tu connais on considérait le produit)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Avr 2010, 15:58
par benekire2 » 20 Avr 2010, 15:58
merci lapras ^^
j'ai regardé vite fait, et je pense que ça fonctionne comme la méthode d'Euclide. Je finirais quand j'aurais du temps .
Une question , toujours sur les nombres premiers, mais pas mal différente :zen: :
Existe-il un polynôme (non nul) à coefficients entiers tel que l'ensemble des valeurs prises par ce polynôme dur N ne soit constitué que de nombres premiers ?
Merci :id:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Avr 2010, 16:07
par Doraki » 20 Avr 2010, 16:07
P(X) = 2 m'a l'air de fonctionner =D
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Avr 2010, 16:09
par benekire2 » 20 Avr 2010, 16:09
Doraki a écrit:P(X) = 2 m'a l'air de fonctionner =D
non constant, j'ai omis de le signaler.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 20 Avr 2010, 16:11
par Matt_01 » 20 Avr 2010, 16:11
Non. C'est vrai que c'est une question légitime, mais ce genre de polynome n'existe pas. Et même plus, l'ensemble des diviseurs premiers des valeurs prises par un polynome non constant est infini.
J'en donne une démonstration ici :
http://forum.prepas.org/viewtopic.php?f=3&t=11726&st=0&sk=t&sd=a&start=765#p288549L'énoncé précis de la propriété à démontrer est juste un peu au dessus (c'est de l'ordre d'un oral d'ENS).
Par contre Euler a exhibé un polynôme qui prend 40 valeurs premières consécutives il me semble.
Le théorème de Tao Green dit aussi que l'on peut trouver, et ce pour n'importe quelle valeur de k, une fonction affine an+b telle que pour un certain p entier, pour n compris entre p et p+k-1 (par valeurs entières), l'ensemble des valeurs prises sont premières.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 20 Avr 2010, 16:47
par nodjim » 20 Avr 2010, 16:47
Moins facile: démontrer qu'il existe une infinité de premiers de la forme 4k+1.
Je n'ai pas la solution pour l'instant.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 20 Avr 2010, 16:56
par lapras » 20 Avr 2010, 16:56
Indice nodgim : utiliser les nombres de fermat : F_n = 2^(2^n) +1 .
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Avr 2010, 17:10
par benekire2 » 20 Avr 2010, 17:10
pour l'existence c'est trivial, je réfléchis à la preuve pour l'infinité ( naturellement)
et merci à vous ;)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Avr 2010, 17:19
par benekire2 » 20 Avr 2010, 17:19
C'est un cas particulier du théorème de Dirichlet il me semble. J'aurais préféré le cas 4k+3 !! ( que je viens de traiter dans l'exercice à la base de ce topic... :zen: )

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Avr 2010, 17:29
par Ben314 » 20 Avr 2010, 17:29
Pour les nombres premiers congrus à 1 modulo p, on peut aussi montrer que, pour tout n, les diviseurs premiers impairs de n²+1 sont tous congrus à 1 modulo 4 (à l'aide du petit théorème de Fermat)...
P.S.
benekire2 a écrit:pour l'existence c'est trivial, je réfléchis à la preuve pour l'infinité ( naturellement)
Tu cherche l'existence et l'infinité de quoi ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Avr 2010, 17:41
par benekire2 » 20 Avr 2010, 17:41
en fait c'est con ce que j'ai dit. Mais c'est en rapport avec les nombres premiers de la forme 4k+1
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Avr 2010, 11:55
par benekire2 » 21 Avr 2010, 11:55
lapras a écrit:Indice nodgim : utiliser les nombres de fermat : F_n = 2^(2^n) +1 .
oui mais l'idéal serait qu'il y ait une infinité de nombres de Fermat premiers ... or ça on n'en sait rien du tout. Toutefois si tu as mis cet indice c'est qu'il doit permettre de conclure :zen:
Enfin je cherche encore ^^
nodgim: Tu as trouvé ?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Avr 2010, 12:23
par benekire2 » 21 Avr 2010, 12:23
Matt_01 a écrit:Par contre Euler a exhibé un polynôme qui prend 40 valeurs premières consécutives il me semble.
Oui C'est n²+n+41 ; très beau polynôme monsieur Euler !!
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 21 Avr 2010, 12:29
par lapras » 21 Avr 2010, 12:29
Benekire : il s'agit en fait de considérer les diviseurs premiers = 1 [4] des F_n.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Avr 2010, 12:36
par Ben314 » 21 Avr 2010, 12:36
Pour l'indic de Lapras, il n'est pas utile de savoir si
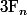
est premier ou pas.
Il suffit de montrer que tout diviseur premier de
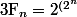})
est forcément congru à 1 modulo
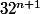
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Avr 2010, 12:46
par benekire2 » 21 Avr 2010, 12:46
oui. C'est pas bête :zen: Fallait-il encore que je le voie ... mais effectivement :)
Merci à vous deux !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Mai 2010, 12:42
par Nightmare » 12 Mai 2010, 12:42
Salut !
Je ressors ce topic, car j'avouerai ne pas voir ou vous voulez en venir avec les nombres de Fermat... Si quelqu'un peut indiquer le cheminement de démonstration.
Cela dit, en utilisant la méthode "usuelle" : S'il existe un nombre fini de nombres premiers congru à 1 mod 4, on considère p le plus grand d'entre eux. On considère alors q premier qui divise (p!)²+1. -1 est un carré mod q et donc (à justifier, loi de réciprocité quadratique par exemple, étude de x->x² dans (Z/qZ)* sinon) q=1 mod[4] contradiction.
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
