Arithmétique groupe zed'n'zed

[vejitoblue]

Salut.
Jai commence à apprendre un peu l'arithmétique modulaire et les groupes.

Ha un exo qui me chagrine un peu. À ma disposition j'ai quelques outils comme Bézout Euclide lemme de Gauss petit Fermat ou la fonction d'Euler... Obligé la réponse se trouve la dedans.... Lexo (mille):

41. Divise 2^36+5^18

J'avais pensé à petit Fermat pour commencer à rendre le truc plus simple. En multipliant par 2^4 le gros chiffre on pourrait se dire que ah ouais 2^40=1(mod41) (vu que 2est premier avec 41 qui est premier aussi. Bref)... Mais j'arrive à rien avec ça.

[Pseuda]

Bonjour,

25+16=41, je ne sais pas si ça peut aider.

[pascal16]

peut être que 36=18+18
et si je ne me trompe pas :
2^7 congru à 5 modulo 41
5^3 congru à 2 modulo 41

"41. Divise 2^36+5^18" -> on dirait la question 41, un point et une question incomplète

[Lostounet]

Salut.
Jai commence à apprendre un peu l'arithmétique modulaire et les groupes.

Ha un exo qui me chagrine un peu. À ma disposition j'ai quelques outils comme Bézout Euclide lemme de Gauss petit Fermat ou la fonction d'Euler... Obligé la réponse se trouve la dedans.... Lexo (mille):

41. Divise 2^36+5^18

J'avais pensé à petit Fermat pour commencer à rendre le truc plus simple. En multipliant par 2^4 le gros chiffre on pourrait se dire que ah ouais 2^40=1(mod41) (vu que 2est premier avec 41 qui est premier aussi. Bref)... Mais j'arrive à rien avec ça.

Salut,
Si on observe comme le dit Pascal que
Alors

De même:


Par contre on peut se demander, comment "observer" si les entiers en jeu étaient plus compliqués. Cela revient, étant donnés deux entiers par exemple a=2 et b= 5, trouver n tel que .
Cette démarche est liée au logarithme discret, qui n'est de mémoire pas un problème facile en général: https://fr.wikipedia.org/wiki/Logarithme_discret
Ainsi qu'au fait de savoir que le "n" n'est pas trop grand non plus.

Aussi une autre démarche (si je me souviens bien), si on avait une puissance de 5 plus grande que 20, serait d'utiliser la loi de réciprocité quadratique d: on a le critère d'Euler, qui dit que car 2 est un carré dans Z/pZ donc son symbole de Legendre est égal à 1.
De même, ce qui signifie que .
Peut-être qu'on pourrait adapter cette méthode.

[aviateur]

Bonjour
Je reviens sur l'indication de @Pseuda que je comprends comme cela:
25+16=41
donc (je corrige un peu pour faire plus simple)

[Pseuda]

25+16=41

Plus explicitement, , donc , donc ?

Pas vu le message d'@aviateur.

[vejitoblue]

Cimer all vous êtes des pros.
En fait ça avait rien de si sorcier, il suffit de dire que 2^36=2 (2^7)^5=18 et 5^18=(5^3)^6=2^6=23 donc que 2^36+5^18=0

++

[vejitoblue]

Salut autres petits exo pour la forme

Le chiffre des unités de 20082008^10?
Donc j'ai fait ça:
En fait je pense qu'on doit travailler dans z10z
20082008=8=-2
-2^10=4(mod10) donc le chiffre des unités est 4

10 divise a^10+1 pour quels a entiers?
Bon déjà ça ressemble à Fermat mais ça fait que lui ressembler.
En gros on veut trouver les entiers a qui ont 9 comme chiffre des unités quand on les élèvent à la puissance 10 et on cherche exprimer ca à l'aide de z10z.
Je crois aussi qu'il y a une élaboration de Fermat quand on est pas modulo un premier. Un truc du genre: a^(p-1)(q-1)=1(mod pq)modulo certaines hypothèses de divisibilité (je m'en souviens car la preuve est easy).

Avec ça on aurait que a^10=-1=9(10)
a^8=1(10) (le Fermat élaboré)
a^2=9(10) (vu que a^8 est inversible)

Par exemple 3et 7 semble fonctionner mais je restreint encore trop l'ensemble de solutions

[Lostounet]

Salut,
Cela marche en regardant les classes résiduelles modulo 10 de proche en proche:
20082008 = 8 [10]

Donc 20082008^10 = 8^10 [10]

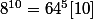
Or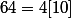 donc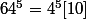



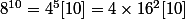
Et 16 = 6 [10] donc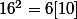 ce qui signifie que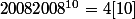

MODIF: Je n'avais pas vu qu'il y avait plusieurs questions dans ton post.

[Lostounet]

a^10+1 est divisible par 10 pour quels a?

Au pire, regarder les classes modulo 10 pour a Tu l'as fait pour 20082008, tu peux bien le faire pour a entre 0 et 9 !

Je trouve a = 3 ou 7 mod 10 aussi

Sinon, a^10 + 1 = 0 mod 10 implique que a^10 + 1 = 0 (mod 2) et a^10 + 1 = 0 (mod 5) (est-ce bien le théorème d'isomorphisme?)
Et on peut regarder ce que donne le petit théorème de Fermat là-dessus mais bon, c'est pas trop évident pour moi ce qui pourrait s'en déduire.

Une autre approche pour le fun:
* D'abord a est impair car si c'est pair, a^n se finit par 0,2,4,6, 8 et + 1 ne fera jamais 0 modulo 10, donc on élimine a = 0,2,4,6,8.
* a n'est pas congru à 5 modulo 10, puisque dans ce cas 5^10 = 5 mod 10 trivialement

* On peut montrer a^10 + 1^10 n'est jamais divisible par (a - 1) ni par (a + 1)

Donc si a^10 + 1 est divisible par 10, alors a - 1 est différent de 10 et a + 1 différent de 10
Donc cela élimine déjà le cas a = 9, mais alors cela élimine-t-il a = 9 (mod 10) ?

Il reste à tester a = 3,7, et 9 éventuellement dans le doute.

[Ben314]

Salut,

Avec ça on aurait que a^10=-1=9(10)
a^8=1(10) (le Fermat élaboré)
...

Le "Fermat élaboré", je suis pas sûr que ce soit bien futé dans un cas pareil.
A mon avis ça marcherais bien plus vite en écrivant on ne peut plus bêtement que
a^10=-1 [10] <=> a^10=-1 [2] et a^10=-1 [5]
(i.e. de dire qu'un entier est divisible par 10 ssi il est divisible par 2 et par 5)

[Pseuda]

Bonsoir,

Pour continuer la solution de Lostounet, pour tester 3, 7, et 9, il suffit de s'arrêter à leurs carrés, la déduction est immédiate.

[vejitoblue]

Merci les gars.

Un autre: mq pour p et q naturels que 2^p-1 et 2^q-1 divisent 2^pq-1

J'avais pensé à deux trucs soit une récurrence soit faire apparaître une somme... À+.

Ben: te moques pas de mon Fermat "élaboré"

[Ben314]

Un autre: mq pour p et q naturels que 2^p-1 et 2^q-1 divisent 2^pq-1

Si tu connait les congruences (et leur propriétés), ça, c'est "con comme la lune" :
Modulo N=2^p-1, ben on a évidement 2^p=1 donc 2^(pq)=1^q=1 ce qui signifie que N divise 2^(pq)-1.

[Lostounet]

Ou alors, par la formule de Bernoulli, est divisible par a - b
Donc est divisible par
est divisible par (2^q - 1)

[vejitoblue]

Ouais j'apprends les congruences j'ai pas fait terminal spé lol
Cimer

En plus je l'avais mais je voulais absolument me retrouver modulo 2^ pq-1, faut que je m'entraîne encore ca doit devenir naturel ces congruences

[Ben314]

Sinon, un peu plus finassou (mais pas beaucoup), c'est de trouver qui est le ppcm(2^p-1 ; 2^q-1).

[Elias]

Un autre: mq pour p et q naturels que 2^p-1 et 2^q-1 divisent 2^pq-1

Attention aux notations: 2^pq-1 se lit.

Sinon, en spé maths, on demande de calculer :


Ce qui prouve que divise
Même chose avec

Une application de ce fait est notamment de voir que si un nombre de Mersenne est premier (i.e. un nombre de la forme avec n entier naturel.non nul ), alors nécessairement n doit être premier.
La réciproque est bien evidemment fausse. Mais on sait alors que si on veut espérer trouver des nombres de Mersenne premiers, il faut aller chercher des exposants premiers.

NB: la recherche de nombres de Mersenne premiers est intéressante car elle permet de trouver des nombres dits parfaits.

[Ben314]

La recherche de nombres de Mersenne premiers est intéressante car elle permet de trouver des nombres parfaits...

...pairs