Arithmétique (exo assez ardu)

[raito123]

Bonsoir,

Je bug sur un exo je veux un petit coup de pouce svp :

Soit n dans IN* on note Pn au nombre premer numéro n tel ( p1=2 , p2=3, p4=5,p5=7,....)!

1/ soit n dans IN*- {1} montrer que ( par absurde )

Merci

++

[tize]

Bonjour raito123,
Suppose pour tout .
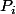
devrait alors être un nombre non premier divisible par l'un des avec

[raito123]

Re,

Et pourquoi elle devrait l'être !!?

En fait je ne vois même pas pourquoi il devrait ne pas être premier !! :cry:

[tize]

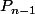
Parce qu'alors le nombre est un nombre entier strictement compris entre et , ça n'est donc pas un nombre premier, il devrait donc être divisible par un nombre premier plus petit : l'un des .

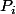
[raito123]

Ok mtn je te suis (je vois même la contradiction) mais suffisait-il pas de supposer que ? car je ne comprend pas pourquoi tu as fais cette supposition !! il se peut qu'il ne soit pas entre et , non ?

[tize]

Je vois que tu as compris.
Oui on peut simplement supposer cela, par contre

il se peut qu'il ne soit pas entre et , non ?

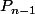
non, est forcément entre et si on suppose

[raito123]

Oui je comprend je vois ce que tu veux dire , merci !!

En fait pour la contradiction on trouve que P_i divise deux nombres succéssifs donc P_i=1 absurde !!

Merci encore !!

++

[tize]

Heu...enfin je voyais plutôt ça comme ça :
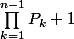
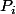
est divisible par un mais n'est pas un nombre entier c'est donc absurde.

[raito123]

Mwé !

ça marche aussi !!