Approximations Successives
19 messages
- Page 1 sur 1
Approximations Successives
bonjour
quelle est le cheminement pour demontrer la convergence de la suite construite lors de l'utilisation de la methode des approximations successives ?
merci
quelle est le cheminement pour demontrer la convergence de la suite construite lors de l'utilisation de la methode des approximations successives ?
merci
c'est en analyse numerique ,c'est chercher le point x tel que f(x) =0 ,et ca revient au meme d'utiliser g(x)=x - f(x) puis de rechercher 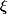 tel que g(
tel que g( 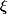 )=
)= 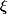 (point fixe )
(point fixe )
alors on construit une suite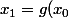 \\ x_2=g(x_1) \\.\\.\\.\\x_{n+1}=g(x_n)) mais la suite (
mais la suite () ne converge pas toujours ,et les conditions de convergences sont :
ne converge pas toujours ,et les conditions de convergences sont :
1_g admet un point fixe
2_g est lipschitzienne
je crois que c'est tout
alors la suite converge
et c'est sur les conditions qu'est ma question
alors on construit une suite
1_g admet un point fixe
2_g est lipschitzienne
je crois que c'est tout
alors la suite converge
et c'est sur les conditions qu'est ma question
on montre que la suite u(n) converge
en montrant que la série u(n+1) -u(n) converge absolument
l u(n+1) -u(n) l =< k l u(n) -u(n-1) l =< ...< k ^(n) l u(1)-u(0) l
or 0
par continuité de g a est point fixe et si b est un point fixe de g
l b-al =l g(b)-g(a) l=< k lb-al donne b = a et unicité du point fixe
c'est le théorème du point fixe dans R qui est complet il en existe bcp de variantes ( espaces compacts par exemple)
en montrant que la série u(n+1) -u(n) converge absolument
l u(n+1) -u(n) l =< k l u(n) -u(n-1) l =< ...< k ^(n) l u(1)-u(0) l
or 0
par continuité de g a est point fixe et si b est un point fixe de g
l b-al =l g(b)-g(a) l=< k lb-al donne b = a et unicité du point fixe
c'est le théorème du point fixe dans R qui est complet il en existe bcp de variantes ( espaces compacts par exemple)
je tente un nouveau truc
pour l'existence du point fixe :
soit g une fonction continue et stable sur [a,b] et posons f(x)= x-g(x) f est continue si g(a)=a ou g(b)=b alors c'est bon sinon on a f(a)=a - g(a) <0 car a 0 car a<=g(b)
pour l'unicite :
avec g contractante on a |g(x)-g(y)|<= k |x-y| ...(*) avec k<1
supposons qu'on a deux point fixe a et a'
alors a=g(a) et a'=g(a')
d'apres (*) on a |g(a)-g(a')|<= k |a-a'|
or |g(a)-g(a')|=|a-a'|
donc |a-a'|<= k |a-a'| et alors |a-a'| (1- k) <= 0 et puisque k<1
|a-a'|=0 donc a=a' donc unicite du point fixe
pour la convergence ,je vais y'arriver ,doucement mais surrement
toute suggestion serait la bienvenue
merci
pour l'existence du point fixe :
soit g une fonction continue et stable sur [a,b] et posons f(x)= x-g(x) f est continue si g(a)=a ou g(b)=b alors c'est bon sinon on a f(a)=a - g(a) <0 car a
pour l'unicite :
avec g contractante on a |g(x)-g(y)|<= k |x-y| ...(*) avec k<1
supposons qu'on a deux point fixe a et a'
alors a=g(a) et a'=g(a')
d'apres (*) on a |g(a)-g(a')|<= k |a-a'|
or |g(a)-g(a')|=|a-a'|
donc |a-a'|<= k |a-a'| et alors |a-a'| (1- k) <= 0 et puisque k<1
|a-a'|=0 donc a=a' donc unicite du point fixe
pour la convergence ,je vais y'arriver ,doucement mais surrement
toute suggestion serait la bienvenue
merci
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
