Approximation differentiable de la valeur absolue

[juliajiul]

Bonjour,

Je suis une débutante dans le domaine donc je ne sais pas trop comment montrer la chose suivante:

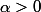
montrer que la fonction , est une approximation différentiable de la valeur absolue.

J'ai essayé de montrer que
Est-ce que je suis sur la bonne piste ? Comment devrais-je essayer de le démontrer?
Merci

[GaBuZoMeu]

On te demande deux choses :
1°) Montrer que est différentiable ( même de classe ).
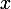
2°) Montrer que est une approximation de la valeur absolue, c.-à-d. majorer par une quantité (indépendante de ) qu'on peut rendre aussi petite qu'on veut en choisissant bien .

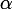
[tournesol]

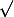
est à valeurs dans ]0;+\infty[ et est Cinfini sur cet intervalle .
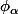
Avec cet info tu peux montrer que est différentiable sur R .
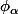
ce qu'on te demande de montrer , c'est que la famille des converge uniformement sur R vers la valeur absolue lorsque tend vers 0.