Approximation décimale

par **jeje56** » 03 Aoû 2009, 17:31

Bonjour,

Je travaille sur l'approximation décimale d'un réel ;
Je justifie l'existence de

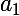
compris entre 0 et 9 et tq :

(

étant la partie entière de x) de la façon suivante :

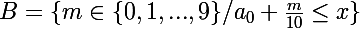
est non vide (contient 0) et majorée par 9 donc admet une borne supérieure qui est le plus grand de ses éléments (car elle est finie)...

Est-ce correct ? 9 majore-il bien B ? Ceci prouve-il aussi l'unicité de

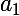
(je ne pense pas...) ?

Merci bcp de votre aide !

par **jeje56** » 03 Aoû 2009, 19:31

Personne pour m'éclairer ?... ;-)

par **Joker62** » 03 Aoû 2009, 20:07

Euhh :/
C'est étrange comme justification.

Je serais plutôt parti du fait que pour tout x réel, x - E(x) est un élément de [0;1[

Donc 10(x-E(x)) est un élément de [0;10[

Suffit de prendre a_1 = E(10(x-E(x))) qui vérifie : a_1 <= 10(x-a_0) < a_1 + 1

par **alavacommejetepousse** » 03 Aoû 2009, 20:26

bonsoir

il y a un problème dans la définition de B car B est inclus dans {0,...9} donc si le plus grand élément a1 de B est 9 rien ne permet d'affirmer que a1 +1 ne vérifie pas l'inégalité
en définissant B comme une partie de N et en remarquant que 9 majore effectivement B il n'y a plus de problème
bien sûr ce que dit joker est plus simple

par **jeje56** » 04 Aoû 2009, 09:59

alavacommejetepousse a écrit:si le plus grand élément a1 de B est 9 rien ne permet d'affirmer que a1 +1 ne vérifie pas l'inégalité

Si a_0=E(x), a_1 ne peut etre plus grand que 9 si ?... Autrement dit a_1+1 ne peut pas vérifier l'inégalité...

Merci à toi !

par **jeje56** » 04 Aoû 2009, 19:33

Personne pour me confirmer tout ça...

par **geegee** » 06 Aoû 2009, 14:02

Bonjour,

http://books.google.fr/books?id=3gZkWHnhOZoC&pg=PA235&lpg=PA235&dq=l'approximation+d%C3%A9cimale+d'un+r%C3%A9el&source=bl&ots=b1jkjJUpDZ&sig=gwm_7XbsgN1M8zLPF5Z0a6wJHY0&hl=fr&ei=R-R6StKVLtSe_gaS1KTkAg&sa=X&oi=book_result&ct=result&resnum=3#v=onepage&q=l'approximation%20d%C3%A9cimale%20d'un%20r%C3%A9el&f=false

C'est juste une recherche web mais il dise que p239 c'est écrit!

par **jeje56** » 06 Aoû 2009, 14:13

Lol, c'est sur ce livre que je travaille !

Merci de ton aide !

Approximation décimale

Approximation décimale

Qui est en ligne