Applicatioon linéaire - base noyau

[novicemaths]

Bonjour

Je cherche à déterminer la dimension et la base du noyau de l'application linéaire ci-dessous.

f(x,y,z)=9x-7y

Là, la dimension du noyau est 1.

Est-ce que la base est ?

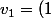Je ne vois pas comment trouver la base du noyau.

Je ne pense pas qu'il soit nécessaire de faire appel au matrice.

A bientôt

[LB2]

Bonjour,

(1) n'est pas un vecteur de l'espace de départ de f (qui est R^3)
Ta réponse est donc non homogène.

Pour trouver une base du noyau on revient simplement à la définition en résolvant le système linéaire
f(x,y,z) = 0.
Ici il faudra faire appel à des inconnues secondaires pour paramétrer ce noyau (on passe d'une équation cartésienne à une équation paramétrique)

[novicemaths]

Donc,

[LB2]

Ton v1 ne vérifie pas f(v1)=0

[novicemaths]

Je vais essayé d'être logique.





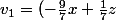Est-ce que là ca va mieux ?

[tournesol]

As tu appris ,novice , que la dimension de l'espace de départ est égale à la somme de la dimension du noyau et de la di mension de l'image . La dimesion de l'image est évidente .

[tournesol]

Ça ne va pas mieux : 9x - 7y + 0z = 0

[LB2]

Je vais essayé d'être logique.





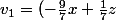Est-ce que là ca va mieux ?

Non pas du tout.

Tu ne résous pas du tout le système linéaire homogène 3x3 correctement.
En fait lorsqu'il y a 3 inconnues et une seule équation, on écrit y =y, z =z, on exprime x en fonction de y et z.
Et tu prends ensuite le v1 qui correspond à x=1, par exemple.

Ici, tu confonds complètement vecteurs et (formes linéaires) coordonnées. Il faut donc tout revoir.

[novicemaths]

Bonjour

Pour que je puisse comprendre, il faut que je sache bien posé le calcul de départ.

Donc, on commence par:





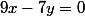
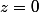
Est ce que l'opération de départ est bien posé ?

A bientôt

[GaBuZoMeu]

Là, tu cherches le noyau de l'application linéaire qui envoie le triplet sur le triplet . Est-ce bien ça que tu veux faire ?

[novicemaths]

non, je cherche la base du noyau.

[GaBuZoMeu]

Du noyau de quelle application linéaire ? Sois précis, l'imprécision amène à raconter un peu n'importe quoi.

[novicemaths]

f(x,yz)=9x-7y

[GaBuZoMeu]

Et donc il s'agit de trouver une base de l'espace des (x,y,z) tels que 9x-7y = 0.
Peux tu résoudre cette équation, autrement dit décrire la forme générale des vecteurs (x,y,z) solutions de cette équation ?

[LB2]

Bonjour

Pour que je puisse comprendre, il faut que je sache bien posé le calcul de départ.

Donc, on commence par:





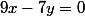
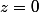
Est ce que l'opération de départ est bien posé ?

A bientôt

Non,

c'est

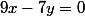
[Carpate]

Suggestions :
Détermine la matrice A (1ligne, 3 colonnes) de l'application exprimée dans la base canonique de
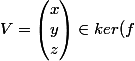est équivalent à soit
Compte-tenu de la relation (1) exprime les composantes de V en fonction de x et de z ( ou de y et de z) et conclus

[novicemaths]

Je dois donner un réponse numérique.

[Carpate]

Je dois donner un réponse numérique

Ben oui, tout finit par des nombres.
Les dimensions du noyau et de l'image de l'application sont ... et ...
En suivant mes indications que trouves-tu comme base du noyau ?
Si tu es bloqué indique au moins ce que tu as fait et où ça bloque ...

[LB2]

La problématique est que novicemaths a beaucoup de mal à résoudre un système linéaire sous déterminé.
Il y a une infinité de solutions, et de plus la dimension du noyau n'est pas 1 mais 2 (mais ça, tu peux le déduire d'une résolution propre).

https://www.maths-france.fr/MathSup/Cou ... stemes.pdf

Voir plus précisément le paragraphe 3.2 pour cet exemple.

[novicemaths]

Voilà, ce que j'ai fais



Je ne vois pas comment continuer. j'ai relu mon livre d'algèbre, il n'y a aucune démonstration de ce genre de calcul.