Applicatioon linéaire - base noyau

[capitaine nuggets]

Bonjour

Je cherche à déterminer la dimension et la base du noyau de l'application linéaire ci-dessous.

f(x,y,z)=9x-7y

Salut !

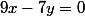
si et seulement si , c'est-à-dire .
Donc :

,

ce qui, en posant , nous donne :

.

Donc est de dimension et une base est donnée par . Si je n'avais pas posé , on aurait eu pour base , mais personnellement, je préfère garder des coordonnées entières quand c'est possible.

[Carpate]

@ novicemaths

Voilà, ce que j'ai fait
https://www.casimages.com/i/20031009142642221.png.html

Tu a osé écrire :

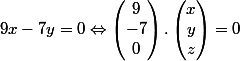
Tu devrais quand même savoir que le produit de 2 matrices n'est défini que si le nombre de lignes de l'une est égal au nombre de colonnes de l'autre !
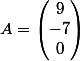
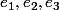
n'est pas la matrice de f dans la base canonique de

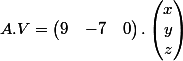
Le produit est lui bien défini et vaut


ainsi
et

[capitaine nuggets]

@ novicemaths

Tu a osé écrire :

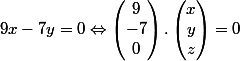
Tu devrais quand même savoir que le produit de 2 matrices n'est défini que si le nombre de lignes de l'une est égal au nombre de colonnes de l'autre !

Je pense que novicemaths a voulu écrire un produit scalaire de deux vecteurs.

[LB2]

Je pense également qu'il s'agit d'un produit scalaire.

Seulement, la notion de produit scalaire n'est absolument pas requise (et même polluante) pour résoudre les problèmes d'algèbre purement linéaire

[Carpate]

Effectivement je n'avais pas imaginé qu'on puisse faire intervenir un produit scalaire dans cet exercice.
Novicemaths ne commente pas beaucoup ses rares calculs.

[novicemaths]

Bonsoir

Là, je ne comprends pas pourquoi vous prenez en compte z dans les calculs.

A bientôt

[LB2]

Bonsoir novicemaths,

as tu pris le temps de lire le paragraphe que je t'ai indiqué sur la résolution des systèmes linéaires?

Cela te donnerait je pense le recul nécessaire pour comprendre et résoudre ton problème.

La résolution de Capitaine Nuggets fonctionne très bien. Celle que je t'avais proposée également.