Applications ouvertes

par **legeniedesalpages** » 09 Mar 2008, 20:40

Bonsoir,

encore une question où je galère.

Soit

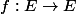
une application telle que pour tous

,
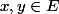
[CENTER]

,

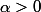
.[/CENTER]

Montrer que

est ouverte.

Merci pour votre aide.

par **ThSQ** » 09 Mar 2008, 23:02

Pas d'autres hypothèses sur f ? (surjectivé ;) ?)

par **legeniedesalpages** » 09 Mar 2008, 23:09

pas à ma connaissance :triste:

par **ThSQ** » 10 Mar 2008, 18:59

f est injective et f^{-1} est C° sur img(f) donc il suffirait de montrer que f(E) est ouvert en fait (ce qui est couvert par le cas f surjective).

Bump ...

par **ffpower** » 10 Mar 2008, 20:13

et si E est connexe,c finalement équivalent a montrer que f est surjective(car si f ouverte,f(E) est ouvert et fermé)

par **yos** » 11 Mar 2008, 11:49

Soit

telle que si

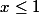
, f(x)=x et sinon f(x)=2x.
C'est pas un contre-exemple?

par **legeniedesalpages** » 12 Mar 2008, 20:42

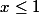
yos a écrit:Soit telle que si , f(x)=x et sinon f(x)=2x.
C'est pas un contre-exemple?

ah si oui effectivement, merci yos et désolé poru lé réponse tardive. :briques:

par **ffpower** » 12 Mar 2008, 20:44

et si f est continue?

Applications ouvertes

applications ouvertes

Qui est en ligne