Bonjour
S'il vous plaît, pouvez-vous m'aider dans cette exercice?
On a f et g 2 endomorphismes de E tels que
f°g=Ide
On doit montrer que
Ker(g°f)=Ker(f) j'ai déjà fait cette question
Et :
Im(g°f)=Im(g) c'est cette question que j'arrive pas à la démontrer..
Merci d'avance
Applications linèaires
10 messages
- Page 1 sur 1
Re: Applications linèaires
Bonjour Hoda,
Peux-tu nous écrire stp la solution que tu as déjà rédigée sur la 1ère question ?
Comme tu le sais maintenant, la méthode s'appelle la double implication.
1) Tu considères un élément quelconque) et tu démontres que
et tu démontres que ) .
.
2) Tu considères en suite un élément quelconque) et tu démontres que
et tu démontres que ) .
.
L'hypothèse doit te servir.
doit te servir.
P. S. : linéaire prend un accent aigu, dans le titre.
Cordialement,
--
Mateo.
Hoda a écrit:
On doit montrer quej'ai déjà fait cette question
c'est cette question que j'arrive pas à la démontrer.
Peux-tu nous écrire stp la solution que tu as déjà rédigée sur la 1ère question ?
Comme tu le sais maintenant, la méthode s'appelle la double implication.
1) Tu considères un élément quelconque
2) Tu considères en suite un élément quelconque
L'hypothèse
P. S. : linéaire prend un accent aigu, dans le titre.
Cordialement,
--
Mateo.
Re: Applications linèaires
Pour 1er question on va procéder par double implication:
Soit x€ker(g°f) , g(f(x))=0 ,f°g(f(x))=0 et donc f(x)=0 x€ker(f)
Soit x€ker(f) . f(x)=0 , g(f(x))=g(0)=0 et donc x€ker(g°f)
Mais je sais que la méthode est double implication mais j'arrive pas à l'appliquer dans la 2eme question
Soit x€ker(g°f) , g(f(x))=0 ,f°g(f(x))=0 et donc f(x)=0 x€ker(f)
Soit x€ker(f) . f(x)=0 , g(f(x))=g(0)=0 et donc x€ker(g°f)
Mais je sais que la méthode est double implication mais j'arrive pas à l'appliquer dans la 2eme question
Re: Applications linèaires
Hoda a écrit:Pour 1er question on va procéder par double implication:
Soit, donc
, donc
et donc
donc
Soitdonc
donc
et donc
Ton raisonnement est juste.
1) Soit
2) Soit
Modifié en dernier par Mateo_13 le 05 Avr 2020, 10:30, modifié 1 fois.
Re: Applications linèaires
Mais je sais pas comment raisonner de la même façon pour la question suivante
Merci^-^
Merci^-^
Re: Applications linèaires
Je viens de modifier mon message précédent :
1) Soit) donc il existe
donc il existe 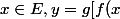]) donc (...).
donc (...).
2) Soit) donc il existe
donc il existe 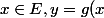) donc (...)
donc (...)
1) Soit
2) Soit
Re: Applications linèaires
Ta deuxième question est déstabilisante car elle contient une spécificité et une généralité .
La généralité c'est que Im (gof) est inclus dans Im(g) pour toute application f de E dans F et toute application g de F dans G . E , F , et G sont des ensembles non vide quelconques .
La généralité c'est que Im (gof) est inclus dans Im(g) pour toute application f de E dans F et toute application g de F dans G . E , F , et G sont des ensembles non vide quelconques .
Re: Applications linèaires
Donc il rest seulment à démontrer que Im(g) est inclu dans Im(g°f) ?
Soit x€Im(g) , x=g(y) , f(x)=y , gof(x)=x et donc x€Im(g°f)
Soit x€Im(g) , x=g(y) , f(x)=y , gof(x)=x et donc x€Im(g°f)
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
