Bonjour,
je vous serez très reconnaissant de bien vouloir m'aider.
Soit K l'application qui à tout polynôme P de R[x] associe le polynôme K(P) = P(X+1) - P(X)
Je cherche à determiner K(1), K(X) , K(X²)
mais je ne vois comment y arriver en remplacant P par 1 , X , X².
Puis
Soit T l'application qui à tout polynôme P de Rn+1[x] dans Rn[X] associe le polynôme T(P) = P(X+1) - P(X)
A quoi correspond T.T ( T point T) et son noyau est il injectif?
En vous remerciant de vouloir gentillement me répondre , je vous souhaite un agréble dimanche
Merci de bien vouloir aider mon petit esprit égaré
Applications linéaires et noyau
3 messages
- Page 1 sur 1
Salut !
Bon, pour la première question c'est trivial K(P)=P(X+1)-P(X)
on est bien d'accord que K : R[X]->R[X]... dans des cas comme ca, pour t'aider, considère la fonction polynômiale associée à K(P) :
K(P):R -> R
x |-> P(x+1) -P(x)
Là, tu devrais t'en sortir.... je te montre pour 1 : Soit P=1 :
pour tout x de R, P(x)=1, donc P(x+1)=1, d'ou K(P)(x)=0
Comme c'est valable pour tout x de R,s'après un théorème dont j'ai oublié le nom (ca fait trop longtemps que j'ai plus joué avec tout ca ;-) ) , tu peux généraliser à X et donc K(1)=0... bien sur, la je rentre énormément dans le détail, tu n'es pas obligé de détailler tout ca, surtout si c'est une première question de devoir/partie...
Bon, pour T.T, j'y réfléchis...
Bon, pour la première question c'est trivial K(P)=P(X+1)-P(X)
on est bien d'accord que K : R[X]->R[X]... dans des cas comme ca, pour t'aider, considère la fonction polynômiale associée à K(P) :
K(P):R -> R
x |-> P(x+1) -P(x)
Là, tu devrais t'en sortir.... je te montre pour 1 : Soit P=1 :
pour tout x de R, P(x)=1, donc P(x+1)=1, d'ou K(P)(x)=0
Comme c'est valable pour tout x de R,s'après un théorème dont j'ai oublié le nom (ca fait trop longtemps que j'ai plus joué avec tout ca ;-) ) , tu peux généraliser à X et donc K(1)=0... bien sur, la je rentre énormément dans le détail, tu n'es pas obligé de détailler tout ca, surtout si c'est une première question de devoir/partie...
Bon, pour T.T, j'y réfléchis...
Bonsoir !
Quand on a un polynôme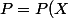=\sum_{i=0}^n a_n X^n) , calculer P(X+1) c'est remplacer X par X+1 dans l'expression de P, ensuite il suffit de faire la différence avec P(X).
, calculer P(X+1) c'est remplacer X par X+1 dans l'expression de P, ensuite il suffit de faire la différence avec P(X).
T.T ça doit correspondre à la composition, donc pour calculer T.T(P), on calcule T(Q) où Q(X) = P(X+1) - P(X) = T(P).
T ne peut pas être injectif car la dimension de l'espace d'arrivée est strictement inférieure à la dimension de l'espace de départ. Et on trouve T(1)=0, T.T(X)=0.
Rq : on ne dit pas « son noyau est-il injectif ? », mais « est-il injectif ? » ou « son noyau est-il nul ? », le noyau c'est un sous-espace de l'espace de départ, l'injectivité c'est défini pour une application.
Quand on a un polynôme
T.T ça doit correspondre à la composition, donc pour calculer T.T(P), on calcule T(Q) où Q(X) = P(X+1) - P(X) = T(P).
T ne peut pas être injectif car la dimension de l'espace d'arrivée est strictement inférieure à la dimension de l'espace de départ. Et on trouve T(1)=0, T.T(X)=0.
Rq : on ne dit pas « son noyau est-il injectif ? », mais « est-il injectif ? » ou « son noyau est-il nul ? », le noyau c'est un sous-espace de l'espace de départ, l'injectivité c'est défini pour une application.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
