Applications linéaires de même noyau
29 messages
- Page 2 sur 2 - 1, 2
Re: Applications linéaires de même noyau
Oui, c'est évident : les restriction de f et g à un même supplémentaire B de leur noyau commun sont des isomorphisme sur leur images respectives et ça te permet d'écrire 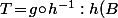\to g(B)) et tu complète T avec (presque) n'importe quoi pour en faire un automorphisme de A.
et tu complète T avec (presque) n'importe quoi pour en faire un automorphisme de A.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Applications linéaires de même noyau
Au niveau purement formel, non vu que  n'est pas bijective.
n'est pas bijective.
Il faut définir une nouvelle fonction\,;\,x\mapsto h(x)) qui elle est bien bijective puis écrire
qui elle est bien bijective puis écrire 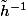
Il faut définir une nouvelle fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Applications linéaires de même noyau
Merci Ben134, et je suis désolé si j’explique mal.
J'ai une autre question mais tu vas pas aimer !!!!
J'ai une autre question mais tu vas pas aimer !!!!
Re: Applications linéaires de même noyau
Est ce qu'il existe d'autres applications 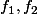 différentes de
différentes de 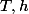 (respectivement) tel que
(respectivement) tel que 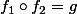
Re: Applications linéaires de même noyau
Ca devient effectivement passablement lassant. . .washwash a écrit:Est ce qu'il existe d'autres applicationsdifférentes de
(respectivement) tel que
Si tu prend pour
C'est évidement le seul "type" de solution si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
29 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
