Applications injective, surjective, bijective

[Swiss_ETHZ]

Bonjour à tous!

Alors voilà je viens de commencer l'uni en physique et je suis bombardé de maths. Quelqu'un pourrait me filer un coup de main pour les exos suivants ou je bloque bien...?

1. Existe t-il des applications injectives, surjectives ou bijectives...:

(i) de {0,11,111} dans {0,1}
(ii) de {x ;) R ;) x^2-4x+3=0} ;) {0,1} dans { n ;) N ;)1 ;) n^3 ;) 100}

2. Soit M un ensemble de même cardinalité que R et A un ensemble dénombrable, disjoint de M. Montrer que M ;) A est de même cardinalité que R.

Merci d'avance pour d'eventuels conseils ou aides

[mathelot]

Bjr,
1. l'idée est simple:

sont équivalents:

(a) il existe une injection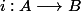
(a') le cardinal de A est inférieur ou égal à celui de B.

(b) il existe une surjection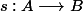
(b') le cardinal de B est inférieur ou égal à celui de A.

(c) il existe une bijection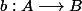
(c') le cardinal de A est égal à celui de B.

et thm de Cantor-Berstein:
si et alors

pour la question (2)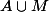 s'injecte dans 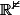donc dans et réciproquement.