Applications de IR² dans IR
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 24 Sep 2012, 22:10
par Luc » 24 Sep 2012, 22:10
capitaine nuggets a écrit: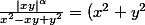 \frac{|xy|^{\alpha -1}}\times {x^2-xy+y^2} \frac{|xy|}{x^2+y^2}\le \frac{x^2+y^2}{2} \frac{|xy|^{\alpha -1}}{x^2-xy+y^2})
Je me suis mal fait comprendre : je parlais de factoriser
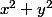
au dénominateur.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 24 Sep 2012, 22:22
par capitaine nuggets » 24 Sep 2012, 22:22
Luc a écrit:Je me suis mal fait comprendre : je parlais de factoriser
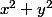
au dénominateur.
Ok :
 \( 1 - \frac{xy}{x^+y^2}\) })
Résultat qui me semble familier parmi ceux qu'on a pu faire.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 24 Sep 2012, 22:29
par Luc » 24 Sep 2012, 22:29
capitaine nuggets a écrit:Ok :
 \( 1 - \frac{xy}{x^+y^2}\) })
Résultat qui me semble familier parmi ceux qu'on a pu faire.
Ça c'est bien parti!

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 24 Sep 2012, 22:32
par capitaine nuggets » 24 Sep 2012, 22:32
Luc a écrit:Ça c'est bien parti!
Or

donc on majore le quotient ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 24 Sep 2012, 22:38
par Luc » 24 Sep 2012, 22:38
capitaine nuggets a écrit:Or

donc on majore le quotient ?
Oui mais n'oublie pas que
1) on travaille en valeur absolues
2) il faut minorer le dénominateur, donc minorer

-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 24 Sep 2012, 22:46
par Sylviel » 24 Sep 2012, 22:46
Globalement sur ce type d'exos je recommande :
- de prendre une suite (x_n,y_n) qui tends vers 0
- de dire qu'il existe une suite r_n tendant vers 0; et une suite theta_n tq
x_n = r_n cos(theta_n)
y_n = r_n sin(theta_n)
- puis tu montres la convergence avec les inégalités naturelles sur les fonctions trigo.
Ca revient à faire le changement de variable proposé plus haut, et c'est sans doute le plus efficace et intuitif dans ces exos.
Ceci étant dis je laisse Luc terminé son guidage :-)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 24 Sep 2012, 22:50
par Luc » 24 Sep 2012, 22:50
Sylviel a écrit:Globalement sur ce type d'exos je recommande :
- de prendre une suite (x_n,y_n) qui tends vers 0
- de dire qu'il existe une suite r_n tendant vers 0; et une suite theta_n tq
x_n = r_n cos(theta_n)
y_n = r_n sin(theta_n)
- puis tu montres la convergence avec les inégalités naturelles sur les fonctions trigo.
Ca revient à faire le changement de variable proposé plus haut, et c'est sans doute le plus efficace et intuitif dans ces exos.
Ceci étant dis je laisse Luc terminé son guidage

Je suis d'accord avec toi mais il n'a pas vu les coordonnées polaires...
Remarquons d'ailleurs qu'on utilise les coordonnées polaires sans le dire, puisque
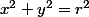
en polaires.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 24 Sep 2012, 22:52
par Sylviel » 24 Sep 2012, 22:52
Ouaip, mais sans les avoir vu il a déjà tous les résultats nécessaire pour les introduire sur une suite...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2012, 22:21
par capitaine nuggets » 25 Sep 2012, 22:21
Bonsoir, connaissant la définition d'une projection sur un ev

parallèlement à

, comment déterminer la matrice représentative

d'une projection

sur le plan
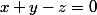
parallèlement à l'axe des abscisses ?
Merci d'avance.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Sep 2012, 18:59
par capitaine nuggets » 27 Sep 2012, 18:59
J'ai eu une autre idée entre temps :
 = 0)
donc

est continue en

?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 27 Sep 2012, 19:05
par Luc » 27 Sep 2012, 19:05
capitaine nuggets a écrit:J'ai eu une autre idée entre temps :
 = 0)
donc

est continue en

?
Ce n'est pas suffisant de montre que
 = 0)
, si tu veux utiliser la caractérisation séquentielle de la continuité, il faut montrer que
 = 0)
pour toute suite
)
tendant vers 0.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Sep 2012, 19:09
par capitaine nuggets » 27 Sep 2012, 19:09
Luc a écrit:Ce n'est pas suffisant de montre que
 = 0)
, si tu veux utiliser la caractérisation séquentielle de la continuité, il faut montrer que
 = 0)
pour toute suite
)
tendant vers 0.
Pourquoi n'est-ce pas suffisant ?
Pourquoi montrer alors ce que tu as écrit avec les suites
)
et
)
?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 27 Sep 2012, 19:22
par Luc » 27 Sep 2012, 19:22
capitaine nuggets a écrit:Pourquoi n'est-ce pas suffisant ?
Pourquoi montrer alors ce que tu as écrit avec les suites
)
et
)
?
Ce n'est pas suffisant pour la même raison que celle que j'ai évoquée plus haut, à savoir : même si tu montres que f(x+ky,x+ky) tend vers 0 pour tout k, cela ne suffira pas : la continuité suivant toute direction n'est pas suffisante, car on peut "s'enrouler" autour du point avec des vitesses différentes suivant les directions.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Sep 2012, 19:24
par capitaine nuggets » 27 Sep 2012, 19:24
Luc a écrit:Ce n'est pas suffisant pour la même raison que celle que j'ai évoquée plus haut, à savoir : même si tu montres que f(x+ky,x+ky) tend vers 0 pour tout k, cela ne suffira pas : la continuité suivant toute direction n'est pas suffisante, car on peut "s'enrouler" autour du point avec des vitesses différentes suivant les directions.
Ok, toutefois, on est en présence d'une forme indéterminée 0/0 !
Je ne vois donc pas comment y parvenir

-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 27 Sep 2012, 19:26
par Luc » 27 Sep 2012, 19:26
Un contre exemple explicite est

définie par
=sin(\frac \pi x))
si (x,y) est différent de (0,0), et f(0,0)=0.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 27 Sep 2012, 19:28
par Luc » 27 Sep 2012, 19:28
capitaine nuggets a écrit:Ok, toutefois, on est en présence d'une forme indéterminée 0/0 !
Je ne vois donc pas comment y parvenir

Repars de
 \( 1 - \frac{xy}{x^+y^2}\) })
et minore

en utilisant

.
Il va falloir utiliser à un moment que

est plus grand que 1.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Sep 2012, 19:40
par capitaine nuggets » 27 Sep 2012, 19:40
Luc a écrit:Repars de
 \( 1 - \frac{xy}{x^+y^2}\) })
et minore

en utilisant

.
Il va falloir utiliser à un moment que

est plus grand que 1.
Je trouve que

-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 27 Sep 2012, 19:40
par Luc » 27 Sep 2012, 19:40
capitaine nuggets a écrit:Je trouve que

Oui c'est bien, que peux-tu en déduire?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Sep 2012, 19:48
par capitaine nuggets » 27 Sep 2012, 19:48
Luc a écrit:Oui c'est bien, que peux-tu en déduire?
j'en déduis alors que :
\(1- \frac{xy}{x^2+y^2}\)}\le 2\times \frac{|xy|^{\alpha } }{(x^2+y^2)})

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Sep 2012, 19:50
par capitaine nuggets » 27 Sep 2012, 19:50
capitaine nuggets a écrit:j'en déduis alors que :
\(1- \frac{xy}{x^2+y^2}\)}\le 2\times \frac{|xy|^{\alpha } }{(x^2+y^2)})
Peut-être qu'on peut utiliser
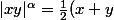^{\alpha} -x^{\alpha} -y^{\alpha}\))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
au dénominateur.
, si tu veux utiliser la caractérisation séquentielle de la continuité, il faut montrer que
pour toute suite
tendant vers 0.
et
?
en utilisant
.
est plus grand que 1.