Applications affines : homotéthie

[jamah3]

Bonjour,

J'ai un probléme avec une des démo de mon cours qui a pour but de montrer que les applications affines dont les applications linéaires associés sont f=kid sont des homotéthies.
Je péche a comprendre la dernière égalité,
comment passe t-on de 1 à 2 , faut il développer et 5 termes sur 6 se suppriment ??
Y a t-il une formule?






merci d'avance

[girdav]

Bonjour,
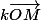
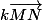
dans le terme 1 on a un vecteur. Le premier point est l'image de par la translation de vecteur et le second est l'image de par la translation de vecteur . Ce vecteur est donc (puisque le second point est l'image du premier par la translation de vecteur ).

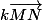
[Ben314]

Salut,
Perso, les notations avec "une grande flèche" et des petites flèches dessous, je trouve ça passablement gonflant, donc je te conseillerais d'utiliser à la place la relation de Chales (cela revient trés EXACTEMENT au même, mais c'est moins chiant à lire) :
f(M)f(N)=M'N'=M'O+ON'=-OM'+ON'=-k.OM+kON=k.MO+k.ON=k.(MO+ON)=k.MN
(ou bien sûr, tu met des flèche partout...)

[jamah3]

Donc l'idée , si j'ai bien compris serait que :



est ce exact?
Je vais essayer de faire des vecteurs avec des points sur une feuille de papier pour me rendre compte

Je vais essayer les 2 , avec les vecteurs et avec chasles

[Ben314]

Je vais essayer les 2 , avec les vecteurs et avec chasles

C'est une super bonne idée qui, à mon avis, te convaincra que :
1) C'est exactement la même chose que l'on écrit mais pas de la même façon.
2) C'est moins "lourd" de l'écrire avec Chasles.

Pour ta question :
" ?"
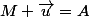
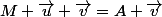
la réponse est oui, vu que le vecteur à gauche du = est celui qui "part" du point pour "arriver" à . C'est donc évidement le vecteur

[benekire2]

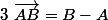
Salut , de toute façon la version "bipoint" avec les flèches et la version "vecteur" sans flèches dit exactement que si A et B sont deux vecteurs alors a partir de cette définition, ce que tu demande est évident.
Sauf erreur ..

[Ben314]

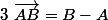
Salut , de toute façon la version "bipoint" avec les flèches et la version "vecteur" sans flèches dit exactement que si A et B sont deux vecteurs alors a partir de cette définition, ce que tu demande est évident.
Sauf erreur ..

Oui, mais certains profs/bouquins n'aiment pas du tout la notation B-A.
Le problème, c'est que, sur une feuille blanche sans axes, si je te place des points A,B,C, lesquelles de ces expressions on un sens et que désignent-elles ?
a) A+B+C
b) A-B+C
c) A+B-2C
Réponses :
a) ne veut rien dire.
b) désigne le point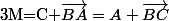
c) désigne le vecteur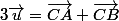

Perso, mon opinion, c'est que, façe à des étudiants "pas trop fortiches", ben on prend un sacré risque qu'ils écrivent des... sacré conneries...

[benekire2]

Ouais je suis d'accord avec toi sur le fond mais c'est quand même la même chose pour moi un point et un vecteur. C'est juste deux manières de visualiser un même concept.

[Doraki]

Non parceque quand on additionne un point avec un point ça ne peut pas donner un point.
Alors que des vecteurs, on peut les additionner pour donner d'autres vecteurs.

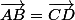
T'as le droit de dire que ABDC est un parallélogramme , ça va.
Mais si tu commences à dire B-A = D-C, ça devient douteux,
et si tu dis que B+C = A+D ou que B+C-A-D = 0, ça ne veut plus rien dire.

Et se donner les moyens d'écrire des trucs qui veulent rien dire, c'est pas une bonne idée.