APPLICATIONS AFFINES EXERCICE

[TiffanieAde]

Bonjour, je suis en Licence 2 de mathématiques, et découvre la géométrie. Notre professeur avance très vite et j'ai encore du mal avec certaines notions. Pourriez vous m'aider pour la résolution de l'exercice suivant :


On suppose que E est de dimension 3 et qu'il est rapporté à un repère cartésien (O, vect(e1), vect(e2), vect(e3)). On considère l'application f de E dans E définie analytiquement par :
x' = x + 6y +3z + 12
y' = -3x -8y -3z - 15
z' = 6x + 12y + 4z + 18

(a) Montrer que f est une transformation affine de E et préciser son application vectorielle associée f flèche.
Déterminer l'application réciproque de f.
(b) Déterminer l'ensemble Inv(f) des points fixes de f.
(c) Déterminer les sous-espaces propres de f flèche.
(d) Soit P le plan d'équation x + 2y + z = 0. Démontrer que tout plan parallèle à P est globalement invariant par f. Quelle est la restriction de f à un tel plan ? En déduire la nature géométrique de f.

Merci beaucoup.

[pascal16]

juste par des considération géométriques :
(a) cours + inversion de la matrice à la calculette
(b) soit à résoudre
x = x + 6y +3z + 12 (1)
y = -3x -8y -3z - 15 (2)
z = 6x + 12y + 4z + 18 (3)
système non inversible, on a (2)*2+(3)=0, la dernière ligne est inutile.
2y +z + 4=0 (1)
x +3y+z+5=0 (2)
on choisi z=t en paramètre
(0) z = t
(1) y= (-4-t)/2=-2-t/2
(2) x=-5-t+ 3(4+t)/2 =1-t/2 <- erreur, c'est 1+t/2
est une droite (et avec (1;-1;2) en vecteur directeur)

(c) vérifier avec eigenvect/eigenvalà la calculette
polynôme caractéristique : x^3+3x²-4=(x+2)²(x-1) -> la fameux det (xID-A)
1 vap simple (déjà fait en b)
-2 vap double ( système équivalent à x+2y+z=0 , tout couple de vecteurs qui engendre ce plan est bon)

(d) Soit P le plan d'équation x + 2y + z = 0.
soit M(x;y;z) de P et M'(x';y';z') son image

on a
x' = x+6y+3z+12 = -2x+12 car x + 2y + z = 0
y' = -2y - 15
z'= -2z +18
(résultat direct avec -2 vap de f fleche)
x'+2y'+z' = -2(x+2y+z)+12-2*15+18 = -2*0+0=0
soit M' dans P

[TiffanieAde]

Merci beaucoup de vos réponse, mais comment dans la question 1, trouver l'application vectorielle associée à f ?

Je suis parvenue à faire le reste de la première question et de la seconde.

[pascal16]

je n'ai utilisé les app affine que pour les EDL avec second membre il y a 20 ans, je ne fais que des déductions logiques, certains corrigerons si je fais une erreur :

x' = x + 6y +3z + 12
y' = -3x -8y -3z - 15
z' = 6x + 12y + 4z + 18

est de la forme X'=AX+B

A est sa partie linéaire, soit :
x' = x + 6y +3z
y' = -3x -8y -3z
z' = 6x + 12y + 4z

au passage , A est inversible
X'-B=AX
A⁻¹(X'-B) =X
soit X = A⁻¹(X') - A⁻¹(B) ce qui semble être un bon candidat pour l'app inverse

[aviateur]

Bonjour
Il me semble bien qu'un calcul de @pascal est faux.
En tout cas la réponse (b) je n'ai pas le même.
C'est la droite qui passe par le point et de direction vecteur invariant (ou propre pour la vp=1) de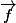
Alors on en déduit directement que f est l'affinité d'axe D dans la direction de P et de rapport -2

[pascal16]

[edit] vep corrigé, c'est ça la flemme de sortir la calculette et de vouloir répondre trop vite.