Application de E*×E* --> B

[Obito31]

Bonjour à tous voilà j'ai un petit problème avec un exercice
Ils nous demande de montrer que l'application
bêta : E*×E* --> B (où B est l'espace des formes bilineaire sur E et E un K-espace vectoriel) n'est pas lineaire
bêta est défini comme sa; bêta(l,m)=l.m où (l.m)(x,y)=l(x).l(y)

Moi j'arrive à la conclusion quelle est lineaire..

bêta est lineaire si elle est lineaire par rapport à ces 2 variable
Donc je définie bêta1 : E* --> B définie par beta1 (l)=l.m où (l.m)(x,y)=l (x).m (y)
Soit l et ľ appartenant à E* et a appartenant à K
Alors beta1 (l+a.ľ)=(l+a.ľ).m
Pour tout x,y appartenant à E on a [(l+a.ľ).m](x,y)= (l+a.ľ)(x).m (y)=[l (x)+a.ľ (x)].m (y)=l (x).m (y)+a.ľ (x).m (y) et donc elle est lineaire par rapport à la 1er variable et pareil pour la 2eme.. ou est-ce que je me trompe ?

[Ben314]

Salut,

bêta est lineaire si elle est lineaire par rapport à ces 2 variable

Je sais pas d'où tu sort ça, mais il faut... oublier tout de suite...

L'application de R² dans R qui à (x,y) associe x+y est effectivement linéaire alors qu'elle n'est absolument pas linéaire par rapport à chacune de ces variables : pour y fixé (non nul), l'application de R dans R qui à x associe x+y n'est pas linéaire.
Et réciproquement, l'application de R² dans R qui à (x,y) associe xy n'est pas linéaire alors qu'elle est linéaire par rapport à chacune de ces variables : pour y fixé (non nul), l'application de R dans R qui à x associe xy est linéaire.

Par contre, une application qui est "linéaire par rapport à chacune de ces variables", ça porte un nom : c'est une application "multilinéaire" (bilinéaire si le nombre de variables est deux).

Et à titre d'exo., peut tu me donner la liste des applications de R² dans R qui sont à la fois linéaire et bilinéaires ?
(avec une preuve bien sûr)

[Obito31]

Ahhh mais oui désolé au faite je suis tellement à fond dans les forme bilineaire et lineaire que je me suis embrouiller..

En même temps ? Hmm
Déjà les forme bilineaire sur de R2 s'écrivent :
f (x1,x2)=f (x1.1,x2.1)=x1.f (1,x2)=x1.y2.f (1,1)=a.x1.x2
Et pour les appliaction lineaire
f (x1,x2)=f (u)=f ((sigma)xi.ei)=(sigma)xi.f (ei)=(sigma)ai.xi ( i allant de 1 à 2 )

C'est bien sa ? Sinon je vois pas comment on peut l'être en même temps désolé

[Ben314]

Y'a qu'une seule façon d'être les deux à la fois : f(x,y)=0 pour tout (x,y).

[Obito31]

Ahhhhhh oui j'allai le dire mais je me suis dit que c'est trop facile xD

[Obito31]

Et donc pour revenir à mon exo

Beta (a.u)=beta (a.l,a.m)=a^2.l.m qui est différent de a.beta (l,m) donc l'application n'est pas lineaire
Et elle n'est pas injective car ker (beta) = {(l,0)U (0,m)} donc différent de 0 et donc pas injective

[Ben314]

Pour une application qui n'est pas linéaire, ça a pas trop de sens de calculer le noyau.
Et si tu avait trouvé que Ker(beta)={0}, ben ça prouverais pas qu'elle est injective.
Par contre, le fait que tu ait plus d'un élément dans Ker(beta), ça prouve que 0 admet au moins deux antécédents et donc qu'elle est pas injective.

[Obito31]

Ah d'accord merci ben le faite que ker (beta)={0} n'implique pas que beta et injective c'est noter !,mais quand j'y pense c'est vrai que sa c'est theoreme de l'algèbre lineaire .. --' je suis bête

[Ben314]

Perso, c'est surtout le fait que, pour les bêtes application de R->R non linéaires, par exemple les fonctions polynômes, ben ça me semble bien clair que de résoudre uniquement f(x)=0, ça te dira pas si f est injective ou pas.

[Obito31]

Oui c'est clair..

[Obito31]

Jaurai aussi une question concernant les matrice des forme bilineaire
Par exemple pour une application lineaire de R3 dans R3 la matrice correspond à 3 vecteur de R3 qui forment l'image on les combinant linéairement après bien sûr ils peuvent être lié etc etc.. je vois ce que le rang veut dire ainsi que le noyau
Mais pour les forme les bilineaire je vois pas à quoi correspond la matrice ni le rang

[Ben314]

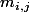Pour une forme bilinéaire de f:ExE->K (corps de base), la définition qu'on prend en général de la matrice associée dans une base B={} c'est M=() où
Donc par exemple, si ta forme bilinéaire est symétrique, ta matrice est symétrique dans n'importe quelle base et réciproquement si la matrice est symétrique dans une base donnée, alors la forme bilinéaire est symétrique.

Mais cette définition "basique" a le mauvais gout de ne pas trop faire le lien avec la définition des matrices d'endomorphismes dans en particulier de ne pas trop expliquer pourquoi on peut calculer le "rang" d'une forme linéaire comme on peut le faire pour un endomorphisme. Donc il y a une deuxième définition, bien sûr équivalente à la première, mais qui demande un peu plus de "bouteille" pour la comprendre :
La donnée d'une forme bilinéaire de f:ExF->G (E,F,G=e.v. quelconque), c'est très exactement la même chose que la donnée d'une application linéaire F:E->L(F,G) (ensemble des application linéaire de F dans G) où, pour tout x de E, F(x) c'est l'élément de L(F,G) défini par f(x)(y)=b(x,y) pour tout y de G. En bref,
Donc par exemple une applications bilinéaires de ExE dans K, c'est la même chose qu'une application linéaire de E dans qui est en fait le dual E* de E. Et comme lorsque l'on se donne une base B de E, cette base induit "canoniquement" une base B* sur le dual E* (la base duale de B), on peut écrire la matrice (au sens usuel) de l'application linéaire F:E->E* dans les bases B et B* et c'est (heureusement) la même chose que la matrice définie précédemment.
De même, lorsque l'on parle du rang d'une application bilinéaire, ça correspond en fait au rang de l'application linéaire de E->E* "canoniquement associée" à la forme bilinéaire de départ donc ça correspond à la dimension su sous espace vectoriel de E* engendré par les différentes formes linéaires .
De même, on peut parler du noyau d'une forme bilinéaire : c'est le noyau de l'application de E->E* associée, c'est à dire l'ensemble des x de E tels que , c'est à dire tels que f(x,y)=0 pour tout y.
Et, par exemple, une forme bilinéaire "non dégénérée", c'est une forme bilinéaire dont le noyau est réduit à {0}.