Bonjour,
Voici deux questions que je n'arrive pas à résoudre.
On a f(x) = 1 + (1/2) integrale de 0 à x de f(t) + f(t^2) dt
On condidère les applications fn(x) avec f0=1 telles que
fn+1 = 1 + (1/2) integrale de 0 à x de fn(t) + fn(t^2) dt
1. Montrer que quelquesoit n appartient à N, fn est une application polynomiale
On démontre ensuite que
f1(x) = x + 1, f2(x)= 1 + x + (x^2/4) + (x^3/6), f3(x) = 1 + x + (x^2/4) + (x^3/24) + (x^4/48) + (x^5/40) + (x^7/84)
2. On pose Dn = sup | fn(x) - fn-1(x) | . Calculer D1 et D2
Merci d'avance pour vos réponses
Application Polynomiale
5 messages
- Page 1 sur 1
je resume :
=1+\frac{1}{2}\int_{0}^{x}\(f(t)+f(t^2)\)dt)
 et
et
=1+\frac{1}{2}\int_{0}^{x}\(f_n(t)+f_n(t^2)\)dt)
au rang 0 c'est donné... si est un polynome, montrons que
est un polynome, montrons que  est un polynome aussi... il se trouve que
est un polynome aussi... il se trouve que  est dérivable de dérivée :
est dérivable de dérivée : +f_n(x^2)\)) qui est (H.R.) un polynome... si
qui est (H.R.) un polynome... si  est un polynome alors
est un polynome alors  aussi (évident).
aussi (évident).
Pour la 2) il doit y avoir une précision, par exemple le sup sur [0;1] sinon c'est toujours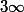
au rang 0 c'est donné... si
Pour la 2) il doit y avoir une précision, par exemple le sup sur [0;1] sinon c'est toujours
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 112 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
