Application matricielle

par **capitaine nuggets** » 20 Oct 2012, 10:19

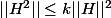
raito123 a écrit:Un résultat général dans M_n(R) est que toutes les normes sont semis-multiplicatives cad il existe k tq . Et là je crois que tu peux facilement conclure.

Ben si on travaillait avec des réels oui, mais là non :cry:

par **raito123** » 20 Oct 2012, 10:27

Et ben c'est la même chose (du moins la même manipulation ). Tu devrais revoir cette partie du cours.

par **capitaine nuggets** » 20 Oct 2012, 16:19

raito123 a écrit:Et ben c'est la même chose (du moins la même manipulation ). Tu devrais revoir cette partie du cours.

Je ne retrouve pas la démonstration.
tu peux me mettre sur la voie stp ?

Est-ce que montrer que f est de classe

est équivalent à dire que f est différentiable ?

par **bentaarito** » 20 Oct 2012, 16:57

être de classe

est plus fort quêtre différentiable (

différentiable)
Néanmoins, l'équivalence est vraie en dimension finie (car linéaire

continue )

par **capitaine nuggets** » 20 Oct 2012, 19:08

Nam 'y a vraiment pas à insister, je ne vois vraiment pas comment montrer que X^2=o(||H|)...
:triste:

bentaarito a écrit:être de classe est plus fort quêtre différentiable ( différentiable)
Néanmoins, l'équivalence est vraie en dimension finie (car linéaire continue )

Ok, merci pour cette précision.

par **raito123** » 20 Oct 2012, 20:58

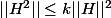
raito123 a écrit:Un résultat général dans M_n(R) est que toutes les normes sont semis-multiplicatives cad il existe k tq . Et là je crois que tu peux facilement conclure.

Donc

et du coup

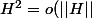ainsi

car c'est une application linéaire en dimension finie donc continue

par **capitaine nuggets** » 21 Oct 2012, 13:37

Ok, merci (ca ne me paraissait pas évident comme ça) :++:

Application matricielle

Qui est en ligne