Dante0 a écrit:Bonjour,
Voila j'ai un petit soucis avec la loi normale
On a étudié la glycémie d'une population d'individus présentant certaines caractéristiques précises, on a obtenu les résultats suivants : 20% des glycémies sont inférieures à 0,82g/l et 30% sont supérieures à 0,98g/l. Si on suppose que la glycémie des individus présentant ces caractéristiques suit une loi normale, déterminez la moyenne et l'écart type de cette loi.
On a le système suivant :
P(X 0,98) = 0,30
Ensuite on arrive au système suivant
 = 0,20)
 = 0,30)
Puis que
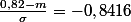
et que

Pourquoi pose-t-on un tel système ? Et comment trouver la valeur de

et

? Je sais que c'est d'après la table des fractiles de la loi normale centrée
réduite mais je ne sais pas comment utiliser cette table...
Merci !

Il faut d'abord bien comprendre ce que signifie la courbe en cloche. Imagine que la leucémie soit représentée par un point sur l'axe horizontal. Si B représente une leucémie de 0.82 gr/l, l'aire sous la courbe à gauche de B est égale à la probabilité d'une leucémie inférieure à0.82, l'aire sous la courbe à droite de B est égale à la probabilité d'une leucémie supérieure à 0.82. Il est évident que l'aire totale sous la courbe est égale à 100%. le point O représente la moyenne m, sa probabilité est 50%. Si D représente une leucémie de 0.98 gr/l, l'aire ACDB est égale à la probabilité d'une leucémie comprise entre 0.82 et 0.98 gr/l.
Pour faciliter les calculs, on va imaginer que les probabilités sont données par une courbe (ou une table) y=f(x). Le point O correspondant à la valeur moyenne m est pris pour origine des abscisses. Une leucémie de valeur X est représentée par un point d'abscisse X-m. On démontre que si on prend pour abscisse le rapport (X-m)/sigma, (appelée valeur réduite), on obtient une courbe unique qui convient à tous les cas, et comme elle est symétrique, on se limitera à la moitié droite (aux valeurs positives de x). La table que tu utilises représente cette courbe. Elle donne pour chaque valeur réduite x la probabilité pour que la leucémie soit inférieure à x.
Comment l'utiliser?
on me dit que la probabilité d'une leucémie supérieure à 0.98 gr/l est 30%. la probabilité d'une leucémie inférieure à 0.98 est donc 70%.
Dans la table je trouve:
probabilité=0.6985, variable réduite=0.52
probabilité=0.7019, variable réduite==0.53
après interpolation:
probabilité=0.70, variable réduite=0.5244 d'où
(0.98-m)/sigma=0.5244
La probabilité d'une leucémie inférieure à 0.82 est 20%. Je raisonne sur le symétrique qui correspond à une probabilité de 80%. Ce chiffre exact n'est pas dans la table, mais je trouve :
probabilité=0.7995 pour variable réduite=0.84
probabilité=0.8023 pour variable réduite=0.85
Je fais une interpolation linéaire (je suppose que tu sais de quoi il s'agit) et je trouve:
probabilité=0.80 pour variable réduite=0.8416 d'où:
(m-0.82)/sigma=0.8416
rappelle s'il y a encore qque chose à clarifier (en particulier si tu as des difficultés avec l'interpolation linéaire).
Dans la pratique, donner une probabilité avec 4 décimales n'a pas de sens vu que la précision des données dépasse rarement 1%, il suffirait donc de faire un interpolation approximative (à vue de nez)

