Application differentiable

[oumou]

Bonjours , je ne suis pas vraiment convaincu des mes reponsees du coup j aimerais savoir si c est correct ou pas .

1) soit f: une fonction bilineaire , on pose H(x,y) = f(-x,-y) , determiner la
differentiellle de la fonction H au point (0,0)?

en composant la fonction f , je trouve DH (0,0) (h,k) = f(h,0) + f(0,k)

2)calculer la differentiellede f,
(A,x) = <Ax.x>
f1 :
(u,v) = <u,v>
f2 :
(A,x) = (Ax, x)
f(A,x) = f1 o f2
Df (A,x)(h,k) = df1(f2(A,x) df2(A,y)(h,k) = df1(Ax,x) ( (hx,x) + (Ak,k) ) = < hx+Ak ,x> + <A(x+k), x+k >


Merci d avance

[Ben314]

Salut,
1) Déjà, je trouve l'énoncé passablement bizarre vu que, si f est bilinéaire alors f(-x,-y)=-f(x,y) par linéarité suivant la première variable puis f(x,-y)=-f(x,y) par linéarité suivant la deuxième variable. Donc H(x,y)=f(x,y).
Ensuite, ta différentielle est assez clairement fausse : une application bilinéaire de R² dans R, ça se présente sous la forme (x,y)->kxy où k est une constante arbitraire dont le gradient au point (x,y) est le vecteur (ky ; ky) et, en (0,0), le gradient (donc la différentielle) est nul.

2) Pour le premier exemple , je comprend pas grand chose à l'énoncé : déjà je vois pas qui est l'ensemble de départ (la notation ne me dit absolument rien) et je vois pas non plus comment est définie la fonction f (ce qui, éventuellement me permettrais de retrouver le domaine de définition)

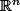
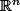
Pour , j'ai l'impression que le domaine de départ, c'est et que la définition de f, c'est (produit scalaire).
Mais l'absence des deux trucs en rouge indispensable à la compréhension du bidule me fait quand même pas mal douter...
Si effectivement c'est bien ça la fonction, ben c'est pas sorcier : il suffit d'évaluer f(u+h,v+k) pour avoir la réponse.

Pour le troisième cas , là je comprend rien à rien, ni l'ensemble de départ ni rien de de ce qu'il y a écrit en dessous.
C'est des définition ?
Si oui, c'est sensé définir quoi ?
Le seul truc que je comprend vaguement, c'est que , qui signifie en particulier que l'image de (A,x) par f est une fonction c'est à dire que f : ???->{ensemble de fonctions}

[oumou]

1) je ne vois pas ce qui cloche sur l enonce (PS: je le fais que recopie )si non il s'avère donc
dh(0,0) (h,k) = df(0,0)(h,k) = 0 nespas ?

2) oh zutt , vraiment desole (je n avais pas relu !! ) ben c est plutot ca :
calculer la differentielle de f, , f (A,x) = <Ax.x>
en composant la fonction f , f = f1 o f2
posons
f1 : f1 (u,v) = <u,v>
et f2 : f2 (A,x) = (Ax, x)
alors
Df (A,x)(h,k) = df1(f2(A,x) df2(A,x)(h,k) = df1(Ax,x) ( (hx,x) + (Ak,k) ) = < hx+Ak ,x> + <A(x+k), x+k >

[Ben314]

Pour le 1), l'énoncé ne "cloche" pas, il est juste "bizarre" vu que H=f.
Et la différentielle de H en (0,0), c'est effectivement l'application (linéaire) nulle.

Sinon, il faudrait bien comprendre que ça : ça ne va pas du tout.
Si f va de ??? dans R, alors à gauche du =, tu as un réel alors que à droite c'est une fonction ce qui évidement complètement incohérent : c'est du même tonneau que d'écrire par exemple Vitesse = 3 Kg.
Bref, soit tu écrit ce qui est une égalité entre deux réels, soit tu écrit ce qui est une égalité entre deux fonctions.

Ensuite, ta notation pour les fonctions, on va dire qu'elle est "vaguement compréhensible", mais ça serait quand même pas con d'utiliser la "notation standard" utilisée par tout le monde :

(et de noter correctement les ensembles)
Donc ici, ça donnerais .

Enfin, ça :

Df (A,x)(h,k) = df1(f2(A,x) df2(A,x)(h,k) = df1(Ax,x) ( (hx,x) + (Ak,k) ) = < hx+Ak ,x> + <A(x+k), x+k >

La première égalité est juste modulo que :
- ça serait pas con d'utiliser le même symbole partout pour les différentielles (D ou d)
- il manque une parenthèse
- entre le df1(f2(A,x) et le df2(A,x), normalement, c'est un symbole "rond" : c'est la composée de deux fonctions (mais comme ça correspond, en terme de coordonnées, au produit de deux matrices, on le met pas toujours)

Par contre, la deuxième est fausse : df2(A,x)(h,k) n'est pas égal à (hx,x) + (Ak,k) mais à (hx,k) + (Ak,k)

[oumou]

1) ah d accord euhh si la fonction f etait definie par exemple de R2 dans R2 alors dh(o,o)(h,k) = f(h,0) + f(0,k) non? (f etant bilineaire biensur )
2)on est d accord que la fonction f2 est bilineaire nespas ? alors comment ca fait que sa differentielle est egale (hx,k) + (Ak,k) ?

[Ben314]

Pour le 1), en fait, j'avais pas assez regardé, df(0,0)(h,k) est effectivement égal à f(h,0)+f(0,k) vu que f(0,h)=f(k,0)=0 (par linéarité).

Sinon, pour le 2), la fonction f2 est clairement non bilinéaire : f(A+B,x) = ( (A+B)x , x) alors que f(A,x)+f(B,x)=(Ax,x)+(Bx,x) =( Ax+Bx , x+x) ( (A+B)x , x)
Et si on veut faire un peu de "théorie", ça vient du fait que (A,x)->Ax est effectivement bilinéaire, mais que (A,x)->x ne l'est pas (en fait elle est linéaire)

[oumou]

Merci infiniment Ben, euhhh si je n abuse pas trop votre gentillesse , est ce que c est possible que vous revoyez SVP mon dernier post sur mon sujet TOPOLOGIE ?