Application de cesaro
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 15 Nov 2007, 19:28
par magnum » 15 Nov 2007, 19:28
bonjour,
soit

une suite réelle tel qu'il existe deux réels a et b tq
)
tende vers a et
)
tende vers b .
démontrer que



tend vers (a+b)/2
Merci .
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Nov 2007, 19:37
par abcd22 » 15 Nov 2007, 19:37
Bonjour,
Et ça ne te donne pas envie de séparer la somme en deux cette question ?
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 15 Nov 2007, 19:39
par magnum » 15 Nov 2007, 19:39
oui, à quelle rang ? Je pense à [n/2] ?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Nov 2007, 20:33
par abcd22 » 15 Nov 2007, 20:33
On a une propriété pour la sous-suite de
)
des indices impairs et une pour les indices pairs donc on sépare suivant les indices pairs et impairs.
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 15 Nov 2007, 21:47
par magnum » 15 Nov 2007, 21:47
ok donc ca donne :
mn = 1/2 (((u1+u3+...+u2k+1)/(n/2))+((u2+u4+...+u2k)/(n/2)))
comment peut-on dire que le membre de droite tend vers a ?
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 15 Nov 2007, 21:49
par magnum » 15 Nov 2007, 21:49
ok merci mais je ne vois pas encore comment utiliser césaro !
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Nov 2007, 00:48
par aviateurpilot » 16 Nov 2007, 00:48
magnum a écrit:ok merci mais je ne vois pas encore comment utiliser césaro !
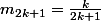\frac{\bigsum_{i=1}^{k}u_{2i}}{k}+\(\frac{k+1}{2k+1}\)\frac{\bigsum_{i=0}^{k}u_{2i+1}}{k+1})
césaro dit que
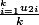
et
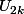
on la meme limite

et
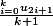
et
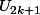
on la meme limite

donc
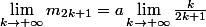+b\(\lim_{k\to +\infty}\frac{k+1}{2k+1}\)=\frac{a+b}{2})
de meme on trouve
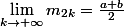
et plus generalement pour

si

alors
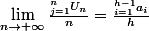
en particulier pour

-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 16 Nov 2007, 01:04
par magnum » 16 Nov 2007, 01:04
en fait je ne comprends pas votre première remarque ''cesaro dit que '' ce n'est pourtant pas césaro sinon il y aurait un 2k au dénominateur ?! non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités