Anneaux quotient et idéaux

[imanebazmaths]

Salut,

Soit A un anneaux unitaire et commutatif
I un idéal de A
f: A --> A/I un morphisme d'anneaux.

On veut calculer Ker f

dans mon livre c'est écrit comme suit:
Ker f={x: x+I =I} = I
pour ka définition du noyau c'est OK mais comment ils trouvent que Ker f=I !!

comme si on a démontré que

si "x est dans I " alors "x+I=I " !!

Merci pour votre aide.

[infernaleur]

Salut,
si tu ne vois pas pourquoi c'est vrai, bah procède par double inclusion (comme d'habitude pour montrer que deux ensembles sont égaux).
Je te fais une inculusion pour t'aider.

Soit
Donc il existe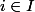 tels que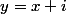
Comme I est un idéal de A il est en particulier un sous groupe additif de A.
Donc

[sofianmakhlouf]

je crois d'abord il faut savoir c'est quoi l'anneau quotient A/I?
il est formé par les classe d'équivalence de la relation d'équivalence R
définie par xRy ssi x-y dans I
f est la surjection canonique
f(x)=cl(x)
x dans le noyau de f ssi f(x)=cl(0 ) ssi x-0=x dans I
d'où ker(f)=I