Anneaux et corps

[aminovic]

bonsoir,
comment monter q'un anneau fini integre est un corps ?
merci d'avance

[Lierre Aeripz]

L'application de multiplication que tu propre n'est en rien une astuce. L'étude de cette application est une méthode générale pour étudier l'inversibilité dans un anneau. Voici un exemple très intéressant.

Soit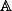 une algèbre associative et unitaire sur le corps , de dimension finie.
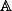Soit une sous-algèbre de , contenant l'unité.
Alors, .
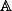Autrement dit, tout élément de , inversible dans est inversible dans .

Preuve
Soit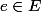 inversible.
On pose .
est une application linéraire. est injective car est inversible. Comme est de dimension finie, est surjective. En particulier,


Avec ce petit théorème, on montre immédiatement que, par exemple, l'inverse d'une matrice triangulaire est triangulaire, l'inverse d'une symétrique symétrique, etc.