Anneau de polynomes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
tac34
- Messages: 5
- Enregistré le: 12 Nov 2008, 19:28
-
 par tac34 » 12 Nov 2008, 19:42
par tac34 » 12 Nov 2008, 19:42
Bonjour,
Voila j'ai un problème a résoudre et vous le soumets:
Soit
 \in \mathbb{Z}\})
Soit maintenant la famille de polynomes
_{k \in \mathbb{N}})
de
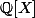
définie par:
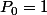
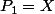
...(X-k+1)}{k!} \qquad \forall k \geq 2)
Apres avoir montrer que A est un sous anneau de
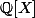
et que

pour tout
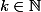
, on nous propose de montrer que tout polynome appartenant à A et de degré n se met sous la forme

avec

Comment faire ? cette question m'a fait penser aux bases dans les sous espaces vectoriels, mais je ne sais comment faire ici dans un sous anneau...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 12 Nov 2008, 20:03
par ThSQ » 12 Nov 2008, 20:03
Les P_k forment une base donc tout polynôme s'écrit

Mézalor
 = a_0)
est entier, P(1) = .....
Au passage il suffit que P(0) ... P(d°P) soit entier.
-
tac34
- Messages: 5
- Enregistré le: 12 Nov 2008, 19:28
-
 par tac34 » 12 Nov 2008, 20:20
par tac34 » 12 Nov 2008, 20:20
Les
_{k \in \mathbb{N}})
forment une base... mais une base dans quel espace ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 12 Nov 2008, 20:34
par ThSQ » 12 Nov 2008, 20:34
Peu importe, Q[X], R[X], C[X], celui qui te plait le plus (Q[X] n'est pas le plus illogique ici ;)) ... ce qui compte c'est de montrer que les a_i sont des zentiers.
-
tac34
- Messages: 5
- Enregistré le: 12 Nov 2008, 19:28
-
 par tac34 » 12 Nov 2008, 20:44
par tac34 » 12 Nov 2008, 20:44
Pour prouver que les
_{k \in \mathbb{N}})
est une base il suffit de prouver que la famille est libre ie que

Mais comment arriver à ce résultat ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 12 Nov 2008, 20:47
par ThSQ » 12 Nov 2008, 20:47
d°P_k = k .
-
tac34
- Messages: 5
- Enregistré le: 12 Nov 2008, 19:28
-
 par tac34 » 12 Nov 2008, 20:52
par tac34 » 12 Nov 2008, 20:52
OK... donc en fait un polynome est nul si et seulement si tous ces coefficients sont nuls hors coefficient de X^n est a_n d'ou a_n=0 et on redéscend ... c'est ca?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 12 Nov 2008, 21:26
par ThSQ » 12 Nov 2008, 21:26
Yep, c'est bien l'idée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
