salut tout le monde.
pouvez vous m'expliquer s'il vous plait pourquoi l'anneau A=[smb]R[/smb][x,y] n'est pas principal ?
dans notre cours on a pris un un idéal
A=R[x,y]
I={P(x,y) appartient A/p(0,0)=0}
donc si I était principal il existerait un polynôme P générateur de I:
soit E appartient A et F appartient A
impliqueP|E et p|F (relation divise)
implique degré(P)<1 (pour X) et degré(P)<1 (pour Y) la je ne comprend pas pourquoi
implique p=cste ,p[smb]appartient[/smb]I [smb]implique[/smb]P=0 impossible et la non plus pourquoi P ne peut etre nul ?
merci pour vos réponses a+
Anneau non principal
2 messages
- Page 1 sur 1
Bonjour, :happy3:
On a :
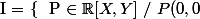 = 0 \ \} = (X,Y) = \{ \ U(X,Y)X+V(X,Y)Y \ / \ (U,V) \in \mathbb{R}[X,Y] \times \mathbb{R}[X,Y] \ \} $)
Par absurde, supposons qu'il existe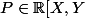 tel que :
tel que :  = (P) $)
Alors : \in \mathbb{R}[X,Y] \times \mathbb{R} [X,Y] $) :
: 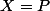 et
et 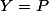 .
.
En écrivant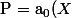 + a_1 (X) Y + ... $) comme un polynôme en
comme un polynôme en  à coefficients dans
à coefficients dans  , la relation :
, la relation : 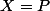 montre que
montre que  , ce qui montre que
, ce qui montre que  ne fait pas intervenir
ne fait pas intervenir  .
.
De même, la relation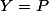 montre que
montre que  ne fait pas intervenir
ne fait pas intervenir  .
.
C'est à dire est un polynôme constant.
est un polynôme constant.
C'est à dire = (1) $)
Par conséquent :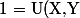X + V(X,Y) Y $) .
.
Or, le terme constant du membre de droite est ,alors que celui du gauche est
,alors que celui du gauche est  ( Contradiction )
( Contradiction )
Donc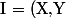 $) n'est pas principal.
n'est pas principal.
Cordialement. :happy3:
On a :
Par absurde, supposons qu'il existe
Alors :
En écrivant
De même, la relation
C'est à dire
C'est à dire
Par conséquent :
Or, le terme constant du membre de droite est
Donc
Cordialement. :happy3:
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
