barbu23 a écrit:Je le définit de deux manières que je cherche à savoir s'il coincide ou pas :
- D'un coté, comme :
.
- De l'autre coté comme :
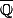
Je ne sais pas. Je ne sais pas précisément par rapport à quelle topologie. :marteau:
Je pense que c'est par rapport à la topologie usuelle de
, et non de celle de
. Parce que, comme l'a dit @mathelot, Si c'est par rapport à la topologie induite sur
, on aura :
. Donc, c'est par rapport à la topologie usuelle de
.
Je cherche plûtot une correspondance bijective entre
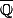
et
, si ce n'est un isomorphisme ou une isométrie. Tous deux donnent :
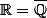
et
. :happy3:
Merci d'avance. :happy3:
Si tu cherches à
définir 
, tu ne peux pas le définir comme l'adhérence
(ce serait l'adhérence dans l'espace que tu cherches).
Si tu définis
comme quotient des suites de Cauchy par les suites convergentes vers 0, tu montreras aisément que
est un corps mais montrer qu'il est complet et que
y est dense sera plus compliqué.
Si tu définis
avec les coupures de Dedekind, il vérifiera naturellement la propriété de la borne supérieure (et en bossant un peu) tu verras que
y sera dense.
Regarde la page wikipedia.
Maintenant si tu disposes de
, peu importe la construction. tu sais que
y est dense et que
est complet. Or
est un complété de
. Donc "l'unicité" du complété nous dira que
et
seront isométriquement homéomorphes (même isomorphes, mais ce n'est pas le théorème du complété qui le dit).
Ta deuxième question était (enfin, je l'ai comprise comme ça): trouver un espace métrique
)
contenant
tel que
et
(pour la topologie de
). Je t'ai montré qu'à isométrie surjective près, alors
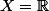
et
est uniforément métriquement équivalente à la valeur absolue sur
.
?
