Anneau / faisceautisation ( sheafification )

[barbu23]

Bonsoir à tous, :happy3:

Connaissez vous la démonstration du théorème qui dit que, si est un anneau intègre, alors : avec parcourant les idéaux premiers et parcourant les idéaux maximaux ? Je l'avais quelques part il y'a quelques temps, mais, je ne me souviens pas où je l'ai vu ?

Merci d'avance. :happy3:

Edit :
J'aimerai aussi avoir l'énoncé et la démonstration du théorème qui dit que si A est un anneau sous certaines conditions, alors : ou ou et parcourant respectivement les idéaux premiers et maximaux de .
Merci d'avance. :happy3:

[Doraki]

je comprends pas comment tu peux parler d'un théorème sans avoir son énoncé.
je peux te le ressortir si tu veux :

Théorème de barbu23 : Si A est la somme directe de ses localisés alors A est la somme directe de ses localisés. (franchement je vois pas beaucoup d'exemples moi)



que A (intègre) est l'intersection de ses localisés, ça doit découler du fait que si x est un élément non nul et non inversible de A alors il y a un idéal maximal M qui le contient (et généralement on prouve ça avec l'axiome du choix si je me gourre pas) et donc tous les trucs de la forme a/x ne sont pas dans le localisé en M

[barbu23]

Merci @Doraki pour ces précisions, même si je n'ai rien compris. :hum: :happy3:
Je ne suis pas trop familier avec l'algèbre commutative. :dodo:
Est ce que quelqu'un peut m'aider sur ces deux questions plus haut svp ?
Merci d'avance. :happy3:

[barbu23]

@Doraki :

J'ai posé ces deux questions, parce qu'il me semble qu'il existe une analogie entre deux choses qui permettent de mieux comprendre les objets intrinsèques qu'on manipule soit en langage des faisceaux ou en langage des schémas : :happy3:

- Si tu es familier avec le langage des faisceaux et pré-faisceaux, alors, le préfaisceau constant : n'est pas un faisceau, mais puisque tout préfaisceau peut se prolonger en un faisceau dans le cadre ce qu'on appelle : faisceautisation ( ou sheafification en anglais ), , alors : le faisceautisé du pré-faisceau est par définition : qui est le faisceau associé au préfaisceau vérifiant certains axiomes simples.
est la notation standard du faisceautisé d'un faisceau quelconque.
Donc, le faisceautisé du préfaisceau est simplement :

- En algèbre abstrait, j'ai vu quelques part dans certains bouquins il y'a longtemps, que : , je ne me souviens pas dans quel cadre j'ai vu ça.

Alors, ne vois tu pas une analogie entre et si on pose ( anneau des entiers relatifs ) ? seulement, dans , est paramétré par des ouverts, alors que dans , n'est paramétré par rien ? Qu'est ce que vous en pensez ? Est ce que c'est vrai ça ?

En plus, en théorie des nombres, j'ai vu un truc comme ça, , ce n'est pas le faisceautisé de , mais c'est autre chose, je ne me souviens pas ce que ça veut dire. Pouvez vous m'en rappeler sa définition ? Ce qui justifie que les notations choisies en mathématiques n'ont pas été choisies aléatoirement, mais ont été choisies avec beaucoup de minutie. svp, qu'est ce que ça veut dire en théorie des nombres, la notation suivante : ? : groupe profini ou complété profini, ou un truc de ce type, je m'en souviens pas.

Merci d'avance pour votre aide. :happy3:

[Doraki]

Comme d'habitude tu dis n'importe quoi.

Ton 1) n'a aucun sens (c'est quoi X ???)
Ton 2) non plus (d'ailleurs Z n'est absolument pas la somme directe de ses localisés)

est le complété de Z, c'est la limite projective des Z/nZ (avec les morphismes de restrictions Z/nZ -> Z/mZ quand m divise n) et c'est aussi (par le théorème des restes chinois) le produit des complétions p-adiques de Z

[barbu23]

Comme d'habitude tu dis n'importe quoi.

Tu es trop hautain, je n'aime pas parler à des types qui te ressemblent. :zen:
Alors, ne vient pas sur mes topics à partir d'aujourd'hui. Je n'ai pas besoin de tes conseils si brillants. :lol3:

[barbu23]

Bonsoir à tous,

A la page : du pdf suivant : http://www-fourier.ujf-grenoble.fr/~peters/FrenchTeaching/m2-95.pdf , on trouve le corollaire suivant :
Un anneau artinien est un produit direct d'un nombre fini d'annaux artiniens locaux : .
malheureusement ne peut pas être considéré comme un anneau artinien car il contient plusieurs suites décroissantes non stationnaires d'idéaux. Par exemple : .
non ?
Donc, n'est pas le produit direct fini d'anneaux locaux. :happy3:

Cordialement.. :happy3:

[barbu23]

Bonjour, :happy3:

Y'a-t-il quelques propriétés intrinsèques communes entre les concepts suivants ou quelques uns d'entre eux :

- complète .
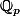
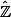
- complète .
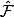
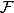
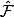
- le faisceautisé d'un préfaisceau complète ce dernier ( i.e : complète )
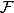
- complète .
- Un espace de Hilbert complète un espace pré-Hilbertien.
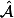
- La tribu complété d'un tribu d'un espace mesuré complète la tribu .
- La mesure de Borel- Lebesgue complète la mesure de Lebesgue.
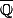
- Le corps des nombres algébriques complète ( Clôture algébrique ).
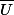
- Si est un ouvert d'un espace topologique , alors le fermé complète .

Merci d'avance.

Edit : Je pense que j'ai mal exprimé ma question :

Je voulais savoir si on peut exprimer toutes les différentes notions de complétion ( ou complétude ) à l'aide de problèmes universelles :

Excuse moi d'avoir choisi un exemple inadéquat ( celui de la tribu borélienne par rapport à la tribu de Lebesgue ). Je voulais simplement parlé de tribu complétée d'une tribu quelconque.

Je modifie donc ma question pour qu'elle deviennent assez claire :

Est ce que tous les complétés d'objets que j'ai cité plus haut représente un foncteur précis ?

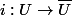
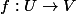
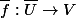
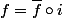
Par exemple, est ce que avec un morphisme à déterminer vérifie la propriété universelle suivante : pour tout ouvert V pour toute application continue , se prolonge en un unique application tel que le diagramme suivant : commute.

La même chose pour le reste des exemples que j'ai cité plus haut.

Merci d'avance.

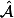
Edit : Pour le cas de la tribu complétée d'une tribu d'un espace mesuré , voiçi comment je vois les choses :
avec à déterminer; vérifie la propriété universelle suivante :
- un espace mesuré, une fonction mesurable, il existe une unique fonction mesurable telle que le diagramme suivant commute : .

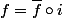
Edit : Je cherche plus précisément, à faire la distinction entre la notion de complétion et la notion de problème universelle. Est ce que toutes les cas de complétions que nous retrouvons en mathématiques : complétion d'un espace vectoriel, ou d'un espace pré hilbertien, ou d'un espace tensoriel ou d'un espace pré-Hilbertien, ou d'un corps ... etc sont des cas particuliers de problèmes universelles, ou c'est le contraire, un problème universelle n'est autre que la notion de complétion ?
Par exemple, est ce que le problème universelle suivant : n'est autre que la complétion de l'espace ? Il me semble que non. C'est pourquoi j'ai besoin de distinguer entre ces deux notions : complétion d'un espace et problème universelle. Avez vous des explications à me faire ?

J'espère que je suis clair maintenant dans mes propos.

Merci d'avance.

[barbu23]

Un petit up pour voir si quelqu'un a une réponse. :happy3:
Merci d'avance. :happy3:

[barbu23]

Un petit up pour voir si quelqu'un a une réponse. :happy3:
Merci d'avance. :happy3:

[barbu23]

Un petit up pour voir si quelqu'un a une réponse. :happy3:
Merci d'avance. :happy3:

[barbu23]

Un petit up pour voir si quelqu'un a une réponse. :happy3:
Merci d'avance. :happy3:

[barbu23]

Est ce que quelqu'un peut me filer un coup de main ?
Merci d'avance. :happy3:

[barbu23]

Une question apparemment stupide : :happy3:
Pour qu'on parle de complétion ou complétude d'un espace, il est nécessaire que l'espace en question soit muni d'une métrique, non ?
Merci d'avance. :happy3:

[mathelot]

Pour qu'on parle de complétion ou complétude d'un espace, il est nécessaire que l'espace en question soit muni d'une métrique, non ?
Merci d'avance.

un espace complet est muni d'une distance
pour laquelle toute suite de Cauchy est convergente. "être suite de Cauchy" n'est pas une notion de topologie,ie, certaines suites peuvent être de Cauchy pour une distance et pas pour , et définissant une même topologie (cf Hauchecorne,"les contre-exemples en mathématiques",Ellipses éditeur ici )

[barbu23]

Bonjour mathelot :

Pour moi, la complétion signifie le fait de combler les trous ou le vide qui manquent à l’intérieur d'un espace. n'est pas complet, il contient des petits espaces qui ne sont pas encore occupés par aucun objet. Pour devenir complet et changer de nom pour en adopter un autre qui est , on a besoin d'une métrique pour les atteindre.
Si on prend un autre exemple où la notion de métrique n'intervient pas, on trouve des espaces incomplets où on a besoin de compléter les espaces vides qu'ils contiennent dans leurs intérieurs.
J'ai cité comme exemple, le faisceautisé d'un préfaisceau. On a pas besoin d'une métrique pour compléter un préfaisceau et le rendre un faisceau. Est ce que donc là, on a comblé des troues dans le préfaisceau qui lui a permis de devenir un faisceau ? Et quels sont ces trous.

Merci d'avance. :happy3:

[mathelot]

le trou est une notion topologique (et je me répète, la complétion , non)

[barbu23]

le trou est une notion topologique (et je me répète, la complétion , non)

D'accord, merci. :happy3:
Donc, la notion de complétion est réductrice. Par contre, si on évoque la notion de complétude ( complété d'un espace ), alors, la complétude est une notion topologique et non métrique. Mais ( je me repète ) le complété d'un préfaisceau est le faisceautisé . qui est un faisceau. Quels sont les éléments qui se trouvent dans et qui ne se trouvent pas dans . Autrement dit, quels sont les objets qui ont occupé les trous de pour devenir ?

Merci d'avance. :happy3:

[mathelot]

soit l'ensemble des rationnels (des fractions)

prouve moi qu'il comporte des "trous" (comme tu veux, mathématique, logique, heuristique).

avant que tu ne répondes, je précise que la logique ne fait pas partie des maths ,pour moi

(tu comprends bien que si on choisit un axiome plutôt qu'un autre, ça prouve
que la logique n'est pas mathématique)

[barbu23]

soit l'ensemble des rationnels (des fractions)

prouve moi qu'il comporte des "trous" (comme tu veux, mathématique, logique, heuristique).

avant que tu ne répondes, je précise que la logique ne fait pas partie des maths ,pour moi.

comporte des trous parce qu'il existe tels que : .
Bref, je n'arrive pas à mettre une liaison entre les choses suivantes :
- Complétion.
- Complétude.
- Solution d'un problème universel.
Je sais juste que la complétion fait partie de la complétude, par contre la complétude est une notion général, et ne se réduit pas à la simple complétion d'après tes explications. :happy3:
Donc, j'ai compris pourquoi :
- complétion complétude.
Mainteant, je cherche à savoir si :
- Complétude Solution d'un problème universel
- Solution d'un problème universelle Complétion
Pour comprendre finalement que :
- Complétude Solution d'un problème universelle Complétion