Anneau des polynomes

[arsene]

Bonjour a tous
je reviens cette semaine avec un autre sujet
Soit R un anneau commutatif et
f(t) = antn + . . . + a1t + a0 de R[t]. si a0 est l unité dans R et
les a1, . . . an nilpotents alors f est inversible.
je ne vois pas le rapport entre la nilpotence des coefficients et l inversibilité de f.
Guidez moi svp
merci

[skilveg]

Salut,

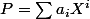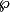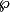Déjà, supposons que est inversible d'inverse . On prend un idéal premier de et on réduit modulo . On sait que 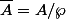est intègre et que 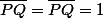, donc en considérant le degré 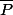est constant. Cela signifie que les coefficients d'indice supérieur à 1 de sont dans 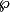pour tout 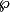, donc dans . Par ailleurs il est immédiat que 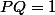impose que soit inversible.

Réciproquement, si est inversible et les autres nilpotents, on peut écrire où tous les coefficients de sont nilpotents. Comme ne comporte qu'un nombre fini de termes, il est nilpotent, et donc 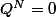pour un bon . Mais alors ce qui conclut.

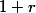L'idée pour la réciproque c'est le fait général suivant: dans un anneau , si est nilpotent, alors est inversible, en développant formellement en série entière.

En espérant répondre à ta question...

[arsene]

donc dans .

merci de ton intervention
c est vrai ke ce n etait qu un sens de la demo qui est posé ici mais sinon c est interessant de comprendre l autre sens
Est ce que tu veux
Le nilradical d un anneau est l intersection de tous ces ideaux premiers?

[skilveg]

c est vrai ke ce n etait qu un sens de la demo qui est posé ici

Ah oui effectivement je me suis un peu emporté... :briques:
Je n'ai pas bien saisi ta dernière question?

[arsene]

dans la demo tu ecris ceci
, donc dans
explique moi stp ce que tu entends par la
je sais que le nilradical d un anneau est l ensemble de ces elements nilpotents
et sinon l egalité ci haut ne me saute pas a l oeil aussitot
je vois une inclusion pas une egalité

[skilveg]

Ah non, ce n'est pas évident! (Quand j'écris je veux dire "l'intersection sur tous les idéaux premiers".)

Comme tu l'as dit, une des deux inclusions est facile.

Supposons que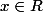 ne soit pas nilpotent et notons 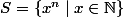. On considère l'ensemble des idéaux de qui ne rencontrent pas , partiellement ordonné par l'inclusion. Cet ensemble est non vide (il contient l'idéal nul), donc par Zorn il admet un élément maximal 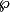, qui par hypothèse ne rencontre pas , et donc ne contient pas . Montrons que 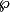est premier, ce qui prouvera que n'est pas dans .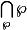

Si et sont hors de 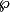, par maximalité de 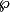il existe deux entiers et tels que et . Mais alors et 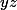ne peut être dans 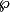car sinon on aurait 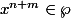ce qui serait absurde. Finalement 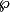est premier.

Remarque: en adaptant la preuve on peut montrer plus généralement que, si est un idéal de , on a
[CENTER]
.
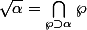[/CENTER]

[arsene]

deux points ne me paraissent pas clair mais bon au moins ja i tiré profit de savoir que c est une egalité meme si je ne peux pas moi meme raisonner pour le demontrer
merci encore