Anneau des Polynômes

[XF63]

Comment peut-on parler d'Anneau des Polynômes quand Kn[X] n'est pas stable pour la loi interne "x" ? Je ne comprends pas !

Merci pour une réponse

[GaBuZoMeu]

Bonsoir,

Qu'est-ce que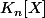 ? Si c'est le sous-espace des polynômes à coefficients dans de degré inférieur ou égal à , personne ne viendra dire que c'est un anneau de polynômes.
Je ne comprends donc pas le sens de ta question. Sois plus clair.

[XF63]

J'entends toujours parler de l'anneau des polynômes.
J'ai cru comprendre, lorsqu'on parle de polynôme, ce n'est jamais un espace infini, c'est toujours l'espace fini des polynômes à coefficients dans K de degré inférieur ou égal à n. Et dans ce cas Kn[X] n'est pas stable pour la loi interne "x" donc ce n'est pas un anneau. Voilà ce que je ne comprends pas !

[mathelot]

bsr,
c'est K[X],+,x l'anneau des polynômes (tout degrés)

[GaBuZoMeu]

J'ai cru comprendre

Eh bien tu t'es fait une fausse idée. la preuve, c'est que l'anneau de polynômes c'est et pas .
L'anneau de polynômes est un espace vectoriel de dimension infinie sur . Quand on fait des exercices d'algèbre linéaire sur des espaces vectoriels de dimension finie, on travaille avec des sous-espaces de dimension finie de en bornant le degré des polynômes considérés : , le sous-espace des polynômes de degré inférieur ou égal à , est de dimension . Si , ce n'est bien sûr pas un sous-anneau de puisqu'il n'est pas stable par multiplication comme tu l'as remarqué.
Lis plus attentivement les définitions. Ça t'évitera de te faire de fausses idées.