Anneau des polynômes et idéaux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 03 Jan 2008, 15:36
par Dyo » 03 Jan 2008, 15:36
Bonjour,
J'ai du mal à comprendre un exercice, si quelqu'un pouvait m'éclairer

Soient

un corps,
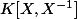
l'anneau des polynômes en

et
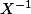
enfin

un idéal de
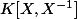
.
1) Montrer que si

engendre
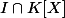
comme idéal de
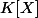
alors

engendre

comme idéal de
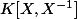
.
La différence entre
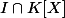
et

, c'est que les coefficients de leurs éléments sont respectivement dans
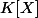
et
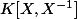
?
2) Déduire que
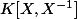
est principal. Je comprends pas bien parce que on a seulement une implication mais ca ne dit pas que tous les
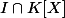
sont principaux...
J'ai pensé à faire par contraposée, mais je n'arrive pas à une contradiction ^^
Merci pour votre aide
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 03 Jan 2008, 17:28
par ThSQ » 03 Jan 2008, 17:28
1) Si
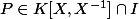
alors
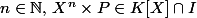
2) conclusion logique de 1
PS Sympa ce cas d'anneau de polynomes à plusieurs variables et principal :happy2:
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 04 Jan 2008, 08:57
par Dyo » 04 Jan 2008, 08:57
Ok je comprends la 1) merci.
Maintenant pour la 2) pourquoi ca découle de la 1) ??
Dans la 1) on a montré : Si

engendre
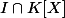
comme idéal de
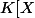
] alors

engendre

comme idéal de
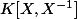
. Rien nous dit que les
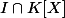
sont engendrés par 1 seul élément... On a juste l'implication que si ils sont engendrés par 1 élément alors...
Tu me comprends ? :p
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Jan 2008, 10:31
par yos » 04 Jan 2008, 10:31
Bonjour.
K[X] serait pas principal?
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 04 Jan 2008, 10:45
par Dyo » 04 Jan 2008, 10:45
Salut Yos,
ah oui, K est un corps => K[X] principal...
Ouhla j'ai du mal à me mettre dedans, merci bien ;)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 04 Jan 2008, 11:02
par ThSQ » 04 Jan 2008, 11:02
Dyo a écrit:K est un corps => K[X] principal.
Que penses-tu de la réciproque Dyo :
A un anneau (commutatif unitaire intègre)
A[X] principal => A est un corps ?
Edit : Tiens d'ailleurs l'hypothèse intègre n'est pas indispensable, elle découle de A[X] principal facilement
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 04 Jan 2008, 11:36
par Dyo » 04 Jan 2008, 11:36
J'ai un exercice où on demandait la réciproque (en plusieurs étapes).
Donc la réciproque est vraie.
A un anneau (commutatif unitaire intègre). Soient
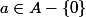
,
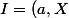)
l'idéal de
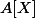
engendré par

et

.
1) Supposer qu'on peut engendrer

par un seul élément. Montrer que

est une unité.
2) Montrer que
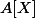
est principal

est un corps.
Voilà ce que j'ai fait :
1)
Supposons
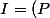)
. On a
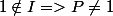
or
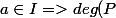 \leq deg(a)=0)
donc
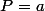
. De plus
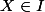
donc
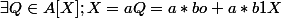
On a
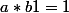
donc
)
.
2)
Si
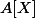
est principal. Comme

est un idéal de
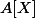
on a
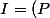)
. Donc d'après 1)
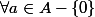
on a :
)
Donc A est un corps.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Jan 2008, 12:29
par leon1789 » 04 Jan 2008, 12:29
Dyo a écrit:1) Supposer qu'on peut engendrer

par un seul élément. Montrer que

est une unité.
Voilà ce que j'ai fait :
1)
Supposons
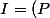)
. On a
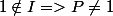
or
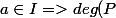 \leq deg(a)=0)
donc
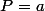
. De plus
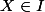
donc
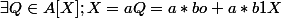
On a
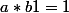
donc
)
.
Pourquoi écris-tu
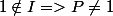
? c'est juste, mais ça sert à quoi ?
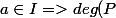 \leq deg(a)=0)
n'implique pas
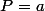
.
Je te propose cela (c'est proche de ta réponse)
Supposons
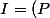)
.
-- L'inclusion
)
donne P divise a et X.
P divise a donc P constant non nul, et ensuite P divise X donc P divise le coeff dominant de X, donc P divise 1, donc P inversible dans A.
-- L'inclusion réciproque
)
donne
 = a*T_o(X)+X*T_1(X))
avec
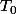
et
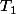
polynômes.
En évaluant en X en 0, on voit que a divise P(0).
-- Conclusion : comme P=P(0) constant inversible dans A et que a divise P(0), on a bien
)
.
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 04 Jan 2008, 12:57
par Dyo » 04 Jan 2008, 12:57
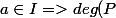 \leq deg(a)=0)
n'implique pas
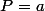
.
J'm'en suis rendu compte en me relisant :briques:
Merci pour ta solution, elle est bien claire :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
par un seul élément. Montrer que
est une unité.
. On a
or
donc
. De plus
donc
On a
donc
.