Analyse synthèse

[mehdi-128]

Bonsoir,

Trouver toutes les applications dérivables sur telles que :

: (*)

Par analyse synthèse. Soit une application qui vérifie l'équation (*) Mais après je n'ai pas d'idées.

[infernaleur]

Salut,
Déjà essaye de trouver f(0)
Ensuite pour x fixé dérive ton égalité par rapport à y

[mehdi-128]

Bonjour, merci pour votre réponse. J'ai trouvé des choses mais une question me taraude : comment savoir si j'ai déterminé toutes les applications vérifiant cette égalité ?

Analyse : supposons que existe.
Dans ce cas, on a :

Si alors donc est la fonction nulle.

Si alors

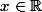
Fixons . Dérivons par rapport à :
Ainsi on a montré :

En particulier pour :

est solution sur de l'équation différentielle :

Les solutions sont les fonctions :

Synthèse :



La fonction nulle vérifie aussi l'égalité.

[aviateur]

Bonjour
Par analogie avec Monsieur Jourdain, tu fais de la mathématiquerie, i.e C'est à dire que tu fais du raisonnement sans le savoir.